Systems of Non-Linear Equations:
  Using the Quadratic Formula (page 6 of 6)

As previously mentioned, sometimes you'll need to use old tools in new ways when solving the more advanced systems of non-linear equations. The example below demonstrates how the Quadratic Formula is sometimes used to help in solving, and shows how involved your computations might get.

• Solve the system:

x² – xy + y² = 21
x² + 2xy – 8y² = 0

This system represents an ellipse and a set of straight lines. If you solve each equation above for y, you can enter the "plus-minus" equations into your graphing calculator to verify this:

x² – xy + y² = 21

y² – xy + (x² – 21) = 0



x² + 2xy – 8y² = 0

0 = 8y² – 2xy – x²

As you can see, I used the Quadratic Formula in each of the original equations, in order to solve for y in terms of x. This gave me equations that I could graph. This technique doesn't come up that often, but it can be a life-saver when you can't seem to solve things any other way.

Oh, and where did those absolute-value bars come from? Recall that, technically, the square root of x² is the absolute value of x. That's how I did that simplification in the next-to-last line above. And this absolute value will matter shortly.

The absolute value of x in the second equation above gives two cases for the values of y:

If x < 0, then | x | = –x, so y =  ^{(x ± 3x)}/₈ = ^x/₂, – ^x/₄

If x > 0, then | x | = x, so y = ^{(x ± 3x)}/₈ = – ^x/₄, ^x/₂.

In either case,  y = – ^x/₄ or y = ^x/₂.

Since I derived these "y=" solution-equations from the second of the original equations, I will plug them into the first equation to solve for some actual numerical values:

If y = – ^x/₄:  Copyright © 2002-2011 Elizabeth Stapel All Rights Reserved

Then, plugging into the "y=" solution-equations above, I get:

If  y = ^x/₂:

Then:

 

Then the four solutions are:

 ,  ,  ,

Warning: Do not try to write the solution points as "" or "", because this is not correct. Not all combinations of these x-value and y-values are solution points. Don't be sloppy; write the solution out correctly.

By the way, the graph of the system looks like this:

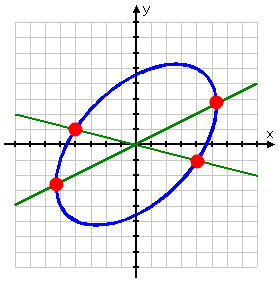
(To graph the ellipse using the traditional methods, you would have to do a "rotation of axes", a process you probably won't see until calculus, if at all.)

By the way, there is another method of doing the algebra for the above exercise, because the quadratic in the second equation happens to be factorable. (This factorability is NOT generally true, but you should try to remember to check, just in case.) If you factor the second equation and solve for x in terms of y, you get:

x² + 2xy – 8y² = 0
(x + 4y)(x – 2y) = 0
x + 4y = 0   or   x – 2y = 0
x = –4y   or   x = 2y

Plug these into the first equation for y, and solve for the x-values.

This last example (the first way I worked it) is about as complicated as these things ever get. But if you plug away and work neatly and completely, you should be able to arrive at the solution successfully. And if you have a graphing calculator (and the time), try doing a quick graph to verify your answers visually.

<< Previous  Top  |  1 | 2 | 3 | 4 | 5 | 6  |  Return to Index

  Copyright © 2002-2012  Elizabeth Stapel   |   About   |   Terms of Use

Contact Us