Return to the Purplemath home page

 

Return to the Lessons Index  | Do the Lessons in Order  |  Print-friendly page

Systems of Non-Linear Equations:
     Advanced Systems (page 5 of 6)

Need a personal math teacher?

The basic process for solving more complicated systems of non-linear equations remains the same as for the previous systems; namely, solve one of the equations for one of the variables, plug that information into the other equation, and solve the resulting one-variable equation. In "real life", advanced systems of non-linear equations probably won't be algebraically solvable. But you can safely expect that the systems they give you in your algebra class will be solvable. However, you may end up needing to use the Quadratic Formula in new ways, and your solutions may involve square roots.

  • Solve the system of nonlinear equations:

      • y = x2
      x2 + (y 2)2 = 4

    From the form of the equations, you should know that this system contains a parabola and a circle.

    According to the graph, there should be three solutions to this system:

     

     

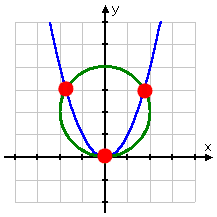
    The solution at the origin is a "neat" one, but the other two intersection points may be messy.

    graph of y = x^2 and x^2 + (y - 2)^2 = 4

    From the first equation, I think I'll plug in "y" for "x2" in the second equation, and solve:

      x2 + (y 2)2 = 4
      y + (y 2)2 = 4
      y + (y2 4y + 4) = 4
      y 2 3y = 0
      y(y 3) = 0
      y = 0,  y = 3

    Now I need to find the corresponding x-values. When y = 0:

      y = x2
      0 = x2
      0 = x

    (This is the solution at the origin that we'd been expecting.) When y = 3:

      y = x2
      3 = x2
      sqrt(3) = x

    Then the solutions are the points (-sqrt(3), 3), (0, 0), and (sqrt(3), 3).

Content Continues Below

  • Solve the following system:

      • 3x2 + 2y2 = 35
      4x2 3y2 = 24

    I can rearrange the first equation to get:

      (x^2)/(35/3) + (y^2)/(35/2) = 1

    This tells me that the first equation is an ellipse. However, rather than graphing this using ellipse formulae, you could also solve to get a "plus-minus" expression that you can graph as two equations:  Copyright 2002-2011 Elizabeth Stapel All Rights Reserved

      y = sqrt((35 - 3x^2)/2)

    (You would plug this into your graphing calculator as two graphs, one graph for the top "plus" part of the ellipse, and another for the bottom "minus" part.) The second equation rearranges as:

      (x^2)/6 - (y^2)/8 = 1

    ...which is an hyperbola. The second equation also solves (for your graphing calculator) as:

      y = sqrt((4/3)x^2 - 8)

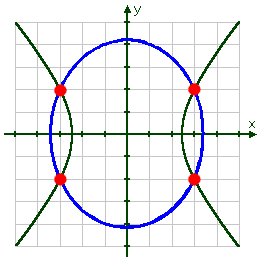
    Whatever format you use (the ellipse and the hyperbola center-vertex forms, or the "plus-minus" for-calculator forms), this system graphs as:

      graph of ellipse and hyperbola

    As you can see, there appear to be four solutions. To find them algebraically, I will choose to solve the second equation for x2 (rather than just x), and plug the resulting expression into the first equation, which I will then solve for y:. (It's okay that I "only" solve for x2, because neither equation has an x-term. There is no need, in this particular case, to do any more solving.)

      4x2 3y2 = 24
      4x2 = 3y2 + 24
      x2 = ( 3/4 )y2 + 6

    Then, subsituting into the first equation for the x2, I get:

      3x2 + 2y2 = 35
      3(( 3/4 )y2 + 6) + 2y2 = 35
      ( 9/4 )y2 + 18 + 2y2 = 35
      9y2 + 72 + 8y2 = 140
      17y2 = 68
      y2 = 4
      y = 2

      Advertisement

    When  y = 2, I get:

      x2 = ( 3/4 )y2 + 6

        = ( 3/4 )(2)2 + 6

        = ( 3/4 )(4) + 6

        = 3 + 6 = 9

      x = 3

    When  y = 2, I get:

      x2 = ( 3/4 )y2 + 6

        = ( 3/4 )(2)2 + 6

        = ( 3/4 )(4) + 6

        = 3 + 6 = 9

      x = 3

    Then the solution is the points (3, 2), (3, 2), (3, 2), and (3, 2), which may also be written as ( 3, 2), since all the "plus-minus" combinations are included.

<< Previous  Top  |  1 | 2 | 3 | 4 | 5 | 6  |  Return to Index  Next >>

Cite this article as:

Stapel, Elizabeth. "Systems of Non-Linear Equations: Advanced Systems." Purplemath. Available
    from https://www.purplemath.com/modules/syseqgen5.htm. Accessed
 

 

Purplemath:

Linking to this site
School licensing

The "Homework
   Guidelines"

Study Skills Survey

Find a local math tutor

  Copyright 2002-2012  Elizabeth Stapel   |   About   |   Terms of Use

 

Contact Us