Ellipses: Introduction
Purplemath
What is an ellipse?
An ellipse, informally, is an oval or a "squished" circle. But an ellipse, technically, is not an oval.
What is the difference between an ellipse and an oval?
An ellipse differs from an oval in that an oval, being egg-shaped, is "flatter" on one end than on the other; an ellipse is equally rounded on each of its ends.
Content Continues Below
An oval can also be called an "egg curve". (Note that the word "ova" means "eggs".)
What is the (physical) definition of an ellipse?
In its original physical sense, an ellipse is the figure you can draw in the sand by the following process:
- Push two sticks vertically down into the sand.
- Take a piece of string and form a loop that is big enough to go around the two sticks and still have some slack.
- Take a third stick, hook it inside the string loop, pull the loop taut by pulling the stick away from the first two sticks.
- Drag that third stick, held vertically, through the sand at the furthest distance the loop will allow.
The resulting shape drawn in the sand is an ellipse.
What are some important terms for ellipses?
Important terms for ellipses are "focus", "vertex", "axis", and "center".
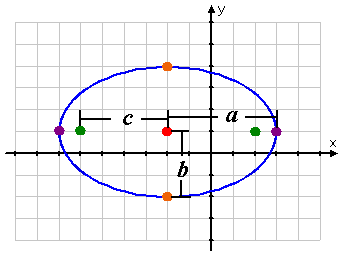
Thinking of the in-the-sand ellipse above, each of the two sticks you first pushed into the sand is a focus of the ellipse; the two together are called foci (FOH-siy). If you draw a line in the sand through these two sticks, from one end of the ellipse to the other, this will mark the major axis of the ellipse. The point midway between the two sticks is the center of the ellipse. If you draw a line through the center, perpendicular to the major axis, this is the minor axis. The points where the major axis touches the ellipse are the vertices of the ellipse; the points where the minor axis touches the ellipse are the co-vertices. The portion of the major axis from the center to the edge is called the semi-major axis; the portion of the minor axis from the center to the edge is called the semi-minor axis.
Affiliate
Advertisement
The distance from the center to either focus of a particular ellipse is the fixed value c. The distance from the center to a vertex is the fixed value a. The values of a and c will vary from one ellipse to another, but they are fixed for any given ellipse.
I keep the meaning of these two letters straight by mispronouncing the phrase "foci for c" as "FOH-ciy foh SEE", to remind me that c relates to the focus. Then the other letter (a) is for the other type of point (the vertex).
The length of the semi-major axis is a and the length of the whole major axis is 2a, and the distance between the foci is 2c.
Okay, so now we've got relationships for a and c, which leads one to wonder, "What happened to b"? The three letters are related by the equation b2 = a2 − c2 or, alternatively (depending on your book or instructor), by the equation b2 + c2 = a2.
(Proving the relationship requires pages and pages of algebraic computations, so just trust me that the equation is true. It can also be shown — painfully — that b is also the length of the semi-minor axis, so the distance across the ellipse in the "shorter" direction is 2b. Yes, the Pythagorean Theorem is involved in proving this stuff. Yes, these are the same letters used in the Pythagorean Theorem. No, this is not the same as the Pythagorean Theorem. Yes, this is very confusing. Accept it, make sure that you memorize the correct relationship before the next test, and then move on.)
Content Continues Below
What is the equation for an ellipse?
For a wider-than-tall ellipse with center at (h, k), having vertices a units to either side of the center and foci c units to either side of the center, the ellipse equation is:
For a taller-than-wide ellipse with center at (h, k), having vertices a units above and below the center and foci c units above and below the center, the ellipse equation is:
An ellipse equation, in conics form, is always "=1".
Note that, in both equations above, the h always stayed with the x and the k always stayed with the y. The only thing that changed between the two equations was the placement of the a2 and the b2. The a2 always goes with the variable whose axis parallels the wider direction of the ellipse; the b2 always goes with the variable whose axis parallels the narrower direction.
Looking at the equations the other way, the larger denominator always gives you the value of a2, the smaller denominator always gives you the value of b2, and the two denominators together allow you to find the value of c2 and the orientation of the ellipse.
Also note that the ellipses we're talked about so far have major axes that parallel either the x-axis or the y-axis. Yes, ellipses can be angled in other directions. No, you will not have to work with that sort of ellipse — at least not until calculus.
What is an ellipse's "eccentricity"?
Ellipses are, by their nature, not perfectly round in the technical sense that circles are perfectly round, and the measure of the amount by which an ellipse is squished away from being perfectly round is called the ellipse's "eccentricity e". The value of an ellipse's eccentricity is given by .
Affiliate
Since the foci are closer to the center than are the vertices, then c < a, so the value of e will always be less than 1. If an ellipse's foci are pulled inward toward the center, the ellipse will get progressively closer to being a circle. Continuing that process, if we let c = 0 (so the foci are actually at the center), this would correspond to e = 0, with the ellipse really being a circle. This tells us that the value of e for a true (non-circle) ellipse will always be more than 0. Putting this together, we see that 0 < e < 1 for any ellipse.
When scientists refer to something (such as the dwarf planet Pluto) as having an "eccentric" orbit, they don't mean that the orbit is quirky or weird; they mean that it's not circular. (In Pluto's case, its orbit actually crosses inside that of Neptune from time to time.) The larger the value of e, the more squished the ellipse.
What is a physical property of ellipses?
A physical property of ellipses is that sound or light rays emanating from one focus will reflect back to the other focus. This property can be used, for instance, in medicine. A patient suffering from, say, gall stones can be placed next to a machine that emits shock waves away from the patient and into an elliptical bowl. The patient is carefully positioned so that the gall stones are at one focus of the ellipse, with a water-filled cushion between the machine and the patient allowing for efficient transmission of the shock waves. The machine emits waves from the other focus of the ellipse; these waves scatter harmlessly from the emitter into the elliptical bowl, bounce back from the bowl, and finally reconcentrate at the other focus (inside the patient). The shock waves reach full power only at the patient's focus, where they smash the stone into pieces small enough that the patient's body will be able to get rid of them on its own. The patient can go home the same day, having been subjected to no invasive surgery.
URL: https://www.purplemath.com/modules/ellipse.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()




