The Quadratic Formula Explained
Purplemath
When would I use the Quadratic Formula?
You can use the Quadratic Formula any time you're trying to solve a quadratic equation — as long as that equation is in the form "(a quadratic expression) that is set equal to zero".
Often, the simplest way to solve "ax2 + bx + c = 0" for the value of x is to factor the quadratic, set each factor equal to zero, and then solve each factor. But sometimes the quadratic is too messy, or it doesn't factor at all, or, heck, maybe you just don't feel like factoring. While factoring is not always going to be successful, the Quadratic Formula can always find the answers for you.
Content Continues Below
The Quadratic Formula uses the "a", "b", and "c" from "ax2 + bx + c", where "a", "b", and "c" are just numbers; they are the "numerical coefficients" of the quadratic equation they've given you to solve.
The Quadratic Formula is derived from the process of completing the square, and is formally stated as:
What is the Quadratic Formula?
The Quadratic Formula is a rule that says that, in any equation of the form ax2 + bx + c = 0, the solution x-values of the equation are given by:
Affiliate
How do I use the Quadratic Formula?
To use the Quadratic Formula, you must:
Arrange your equation into the form "(quadratic) = 0".
Arrange the terms in the (equation) in decreasing order (so squared term first, then the x-term, and finally the linear term).
Pull out the numerical parts of each of these terms, which are the "a", "b", and "c" of the Formula.
Plug these numbers into the formula.
Simplify to get your answers.
Advisories: The "2a" in the denominator of the Formula is underneath everything above, not just the square root. And it's a "2a" under there, not just a plain "2". Make sure that you are careful not to drop the square root or the "plus/minus" in the middle of your calculations, or I can guarantee that you will forget to "put them back in" on your test, and you'll mess yourself up. Remember that "b2" means "the square of ALL of b, including its sign", so don't leave b2 being negative, even if b is negative, because the square of a negative is a positive.
In other words, don't be sloppy and don't try to take shortcuts, because it will only hurt you in the long run. Trust me on this!
What is an example of using the Quadratic Formula?
Solve x2 + 3x − 4 = 0
This quadratic happens to factor, which I can use to confirm what I get from the Quadratic Formula. The Formula should give me the same answers.
x2 + 3x − 4 = (x + 4)(x − 1) = 0
...so I already know that the solutions are x = −4 and x = 1.
Now, what would my solution look like in the Quadratic Formula? Using a = 1, b = 3, and c = −4, my solution process looks like this:
So, as expected, the solution is x = −4, x = 1.
For this particular quadratic equation, factoring would probably be the faster method. But the Quadratic Formula is a plug-n-chug method that will always work. Having "brain freeze" on a test and can't factor worth a darn? Use the plug-n-chug Formula; it'll always take care of you!
Content Continues Below
How does the Quadratic Formula relate to x-intercepts?
The solutions to the quadratic equation, as provided by the Quadratic Formula, are the x-intercepts of the corresponding graphed parabola.
How? Well, when y = 0, you're on the x-axis. The x-intercepts of the graph are where the parabola crosses the x-axis. You're applying the Quadratic Formula to the equation ax2 + bx + c = y, where y is set equal to zero.
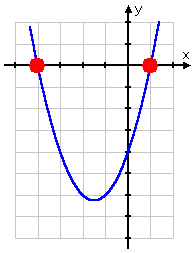
Looking at the above example, there were two solutions for the equation x2 + 3x − 4 = 0. This tells us that there must then be two x-intercepts on the graph. Graphing, we get the curve below:
Advertisement
Affiliate
As you can see, the x-intercepts (the red dots above) match the solutions, crossing the x-axis at x = −4 and x = 1. This shows the connection between graphing and solving: When you are solving "(quadratic) = 0", you are finding the x-intercepts of the graph. This can be useful if you have a graphing calculator, because you can use the Quadratic Formula (when necessary) to solve a quadratic, and then use your graphing calculator to make sure that the displayed x-intercepts have the same decimal values as do the solutions provided by the Quadratic Formula.
Note, however, that the calculator's display of the graph will probably have some pixel-related round-off error, so you'd be checking to see that the computed and graphed values were reasonably close; don't expect an exact match.
Solve 2x2 − 4x − 3 = 0. Round your answer to two decimal places, if necessary.
There are no factors of (2)(−3) = −6 that add up to −4, so I know that this quadratic cannot be factored. I will apply the Quadratic Formula. In this case, a = 2, b = −4, and c = −3:
Then the answer is x = −0.58, x = 2.58, rounded to two decimal places.
Can I round my answers from the Quadratic Formula?
In general, no, you really shouldn't; the "solution" or "roots" or "zeroes" of a quadratic are usually required to be in the "exact" form of the answer. You can use the rounded form when graphing (if necessary), but "the answer(s)" from the Quadratic Formula should be written out in the (often messy) "exact" form.
In the example above, the exact form is the one with the square roots of ten in it. If you're wanting to graph the x-intercepts or needing to simplify the final answer in a word problem to be of a practical ("real world") form, then you can use the calculator's approximation. But unless you have a good reason to think that the answer is supposed to be a rounded answer, always go with the exact form.
Reinforcing the concept: Compare the solutions we found above for the equation 2x2 − 4x − 3 = 0 with the x-intercepts of the graph:
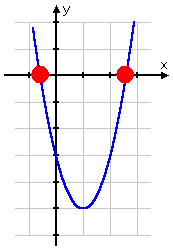
Just as in the previous example, the x-intercepts match the zeroes from the Quadratic Formula. This is always true. The "solutions" of an equation are also the x-intercepts of the corresponding graph.
URL: https://www.purplemath.com/modules/quadform.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()