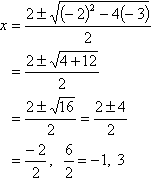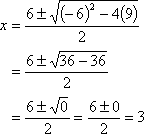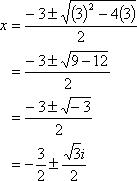The Quadratic Formula: The Discriminant and Graphs
Purplemath
-
Solve x2 + 2x = 1. Round your answer(s) to two decimal places.
Wait! I cannot apply the Quadratic Formula yet!
The Formula only applies once I have "(quadratic) = 0", and I don't have that yet here. So the first thing I have to do is move the 1 over to the left-hand side of the equation, so I'll have "= 0" on the right-hand side.
Doing so gives me the following equation:
x2 + 2x – 1 = 0
Content Continues Below
Letting a = 1, b = 2, and c = –1, the Quadratic Formula gives me:
Then the solutions are:
x = –2.41, x = 0.41, rounded to two decimal places.
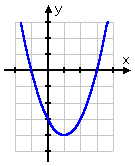
Here's the graph of the associated function, y = x2 + 2x − 1:
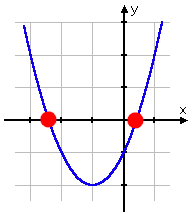
The x-intercepts (that is, the solutions from above) are marked in red. These are the spots where the associated function, y, was equal to zero.
Affiliate
Note that the x-intercepts of the associated function match with the solutions to the original equation. And recall that the value of the discriminant (the part inside the square root in the Quadratic Formula) was positive.
This relationship between the value inside the square root (the discriminant), the type of solutions (two different solutions, one repeated solution, or no rea solutions), and the number of x-intercepts (on the corresponding graph) of the quadratic is summarized in the following table:
← swipe to view full table →
quadratic equations and their solutions |
||
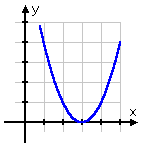
x2 – 2x – 3 = 0 |
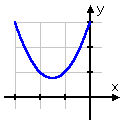
x2 – 6x + 9 = 0 |
x2 + 3x + 3 = 0 |
|
|
|
a positive number inside the square root |
zero inside the square root |
a negative number inside the square root |
two distinct real-number solutions |
one (repeated) real-number solution |
no real-number solutions |
associated functions and their graphs |
||
y = x2 – 2x – 3 |
y = x2 – 6x + 9 |
y = x2 + 3x + 3 |
|
|
|
two distinct x-intercepts |
one (repeated) x-intercept |
no x-intercepts |
What is the point of the above table? The point is that there is a clear and consistent connection between solutions of quadratic equations (where you've got "(quadratic) = 0") and the graphs of the associated functions (which will be "y = (quadratic)"); namely, that the real solutions of the equation will be the x-intercepts of the graph.
Content Continues Below
So if you're wanting to check your solutions to a given quadratic equation, plug the associated quadratic function into your graphing calculator, and check the graph. Does the graph cross the x-axis at your solution points? Then you probably have the right answer. Did you get a repeated solution (that is, a soluton with zero inside the square root), but the graph doesn't touch the axis at all? Then your solution is probably wrong. And so forth. Use the graphs to check the solutions.
Probably the most important thing to remember when using the Quadratic Formula (other than the Formula itself, which you should memorize) is that you must do each step clearly and completely, so you don't lose your denominators or plus-minuses or square roots. Don't skip stuff, and you should do fine.
Warning: If you get in the habit of "forgetting" the square root sign until the end when the back of the book "reminds" you that you "meant" to put it in, I'll bet good money that you'll mess up on your test. If you get in the habit of "forgetting" the plus/minus sign until the answer in the back "reminds" you that it belongs in there, then you will almost certainly miss every single problem where the answer doesn't have a square root symbol in it to "remind" you to put the plus/minus sign back in.
Affiliate
Also, if you get sloppy with the denominator "2a", either by forgetting the "a" or by not dividing the entire numerator by this value, you will consistenly get the wrong answers.
In other words, if you get in the habit, on your homework, of being lazy, then any time your answer is supposed to be something like "x = 5 ± 10", you will put down "x = 5 + 10 = 15", and will have no idea how the book (or test) got the second answer of "x = –5". That is, until you magically "remember", and slap the "plus-minus" back in there. Or you'll be completely confused as to why their answer is off by a factor from yours, until you magically "remember" to fix the denominator.
But "magic" won't happen on the next test. So get in the habit, now, of using the Formula correctly.
I've been grading homework and tests for too many years to be kidding about this. Really, truly; you want to do your work neatly and completely every single time!
You can use the Mathway widget below to practice finding the median. Try the entered exercise, or type in your own exercise. Or try entering any list of numbers, and then selecting the option — mean, median, mode, etc — from what the widget offers you. Then click the button to compare your answer to Mathway's.
Click "Tap to view steps" to be taken to the Mathway site.
URL: https://www.purplemath.com/modules/quadform.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()