Straight Lines from a Quadratic Equation?
Purplemath
Under what condition does a quadratic equation actually graph as two straight lines?
A quadratic equation will graph as two straight lines under the condition that the quadratic be factorable into two linear factors. In other words, the quadratic must factor as follows:
(ax + by + c)(dx + ey + d) = 0
In every other case, the quadratic graphs as some sort of conic, and thus a curved line or lines. (technical info)
In my lesson on solving systems of non-linear equations, I included in one example a second-degree equation where the quadratic actually graphed as two straight lines (here). The equation was this:
x2 + 2xy − 8y2 = 0
Don't all second-degree equations model conics?
In general, quadratic (that is, second-degree) equations are conic sections (that is, they are slices taken from two cones placed nose-to-nose), and they graph as curvy lines.
However, if you imagine cutting perpendicularly straight down through the cones, passing through the point where the two cones touch, the graph of the section will represent the straight sides of those cones; that is, they'll be straight lines.
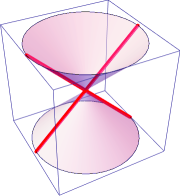
So, in this particular context, straight lines *can* be conic sections, but only if they come in pairs from factoring a quadratic equation.
But don't just take my say-so; let's do the algebra.
- Show that x2 + 2xy − 8y2 = 0 represents two straight lines.
In order for this quadratic to actually represent two straight lines, I know that this quadratic must factor. I'll need factors of −8 that add to +2; I'll use −2 and +4:
x2 + 2xy − 8y2 = 0
(x − 2y)(x + 4y) = 0
x − 2y = 0 ⇒ y = (½)x
x + 4y = 0 ⇒ y = −(¼)x
So the one quadratic equation actually factors as two straight lines whose equations are:
How can I combine two straight lines' equations inside a quadratic?
To combine two straight-line equations into one quadratic equation:
- Rearrange the straight-line equations to have zero isolated on one side of the "equals" sign.
- Multiply the two straight-line equations. Remember that the result is still equal to zero.
- Simplify the quadratic expression, if needed.
We can do this with any two straight lines.
- Find the quadratic equation which models the following two straight lines:
y = 3x − 1
y = −x − 2
To combine these two straight lines into one quadratic equation, I first need to get the line part on one side of the "equals" sign, with zero on the other:
y = 3x − 1 ⇒ 0 = 3x − y − 1
y = −x − 2 ⇒ x + y + 2 = 0
Now I need to multiply these together.
I started by making both of the line equations equal to zero. Then I multiplied them. Multiplying zero by zero gives me zero, so the above expression can be set equal to zero to create my quadratic equation for two straight lines:
3x2 + 2xy − y2 + 5x − 3y − 2 = 0
Why didn't my textbook or instructor ever mention this case for conics?
A pair of straight lines, when viewed as a conic section, is called a degenerate conic, in the (mathematical) sense of having taken a situation (being the two nose-to-nose cones) and finding the least interesting thing you can with it. Just as a point is a degenerate circle (with a radius of zero), so two straight lines are a degenerate conic.
So they probably didn't feel like bothering to mention this. Or maybe, like me, they'd never before heard of this.
© 2024 Purplemath, Inc. All right reserved. Web Design by 