Conics: An Overview
Purplemath
Conic sections are the curves which can be derived from taking slices of a "double-napped" cone. A double-napped cone, in regular English, is two cones "nose to nose", with the one cone balanced perfectly on the other.
What are "sections"?
"Section" here is used in a sense similar to that in medicine or science, where a sample (from a biopsy, for instance) is frozen or suffused with a hardening resin, and then extremely thin slices (that is, sections) are shaved off for viewing under a microscope.
How do conic curves come from cones?
If you think of the double-napped cones as being hollow (say, made of cardboard), the curves we refer to as "conic sections" are the curves that result when we section, or slice, the cones at various angles. In other words, imagine taking that cardboard nose-to-nose cone construction and cutting across it with a hacksaw; those raw cut edges represent the curve which we call a conic section.
(To be a proper "section", you'd need to take a very thin slice of cardboard out of our construction, but that's not strictly necessary. The concept represented by that raw edge is what matters here.)
There are plenty of sites and books with pictures illustrating how to obtain the various curves through sectioning, so I won't bore you with more pictures here. And there are books and entire web sites devoted to the history of conics, the derivation and proofs of their formulas, and their various applications. I will not attempt to reproduce that information here.
This lesson, and the conic-specific lessons to which this page links, will instead concentrate on: finding curves, given points and other details; finding points and other details, given curves; and setting up and solving conics equations to solve typical word problems.
What are some basic conics terms that I should know?
There are some basic terms that you should know for this topic:
- center: the point (h, k) at the center of a circle, an ellipse, or an hyperbola.
- vertex (VUR-teks): in the case of a parabola, the point (h, k) at the "end" of a parabola; in the case of an ellipse, an end of the major axis; in the case of an hyperbola, the turning point of a branch of an hyperbola; the plural form is "vertices" (VUR-tuh-seez).
- focus (FOH-kuss): a point from which distances are measured in forming a conic; a point at which these distance-lines converge, or "focus"; the plural form is "foci" (FOH-siy).
- directrix (dih-RECK-triks): a line from which distances are measured in forming a conic; the plural form is "directrices" (dih-RECK-trih-seez).
- axis (AK-siss): a line perpendicular to the directrix passing through the vertex of a parabola; also called the "axis of symmetry"; the plural form is "axes" (ACK-seez).
- major axis: a line segment perpendicular to the directrix of an ellipse and passing through the foci; the line segment terminates on the ellipse at either end; also called the "principal axis of symmetry"; the half of the major axis between the center and the vertex is the semi-major axis.
- minor axis: a line segment perpendicular to and bisecting the major axis of an ellipse; the segment terminates on the ellipse at either end; the half of the minor axis between the center and the ellipse is the semi-minor axis.
- locus (LOH-kuss): a set of points satisfying some condition or set of conditions; each of the conics is a locus of points that obeys some sort of rule or rules; the plural form is "loci" (LOH-siy).
You may encounter additional terms, depending on your textbook. Just make sure that you understand the particular terms that come up in your homework, so you're prepared for the test.
One very basic question that comes up pretty frequently is "Given an equation, how do I know which sort of conic it is?" Just as each conic has a typical shape:
horizontal parabola
vertical parabola
hor. hyperbola
vertical hyperbola
circle
vertical ellipse
...so also each conic has a "typical" equation form, often along the lines of the following:
parabola: Ax2 + Dx + Ey = 0
hyperbola: Ax2 − Cy2 + Dx + Ey + F = 0
circle: x2 + y2 + Dx + Ey + F = 0
ellipse: Ax2 + Cy2 + Dx + Ey + F = 0
These equations can be rearranged in various ways, and each conic has its own special form(s) that you'll need to learn to recognize, but some characteristics of the equations above remain unchanged for each type of conic.
If you keep these consistent characteristics in mind, then you can run through a quick check-list to determine what sort of conic is represented by a given quadratic equation.
What's a quick way to tell what curve an equation represents?
Given a general-form conic equation in the form Ax2 + Cy2 + Dx + Ey + F = 0, or after rearranging to put the equation in this form (that is, after moving all the terms to one side of the "equals" sign), this is the sequence of tests that will tell you what type of curve will be graphed by a given conics equation:
- Are both variables squared?
No: It's a parabola.
Yes: Go to the next test....
- Do the squared terms have opposite signs?
Yes: It's an hyperbola.
No: Go to the next test....
- Are the squared terms multiplied by the same number?
Yes: It's a circle.
No: It's an ellipse.
- Classify the following equations according to the type of conic each represents:
A) 3x2 + 3y2 − 6x + 9y − 14 = 0
B) 6x2 + 12x − y + 15 = 0
C) x2 + 2y2 + 4x + 2y − 27 = 0
D) x2 − y2 + 3x − 2y − 43 = 0
A) Both variables are squared, and both squared terms are multiplied by the same number, so this is a circle.
B) Only one of the variables is squared, so this is a parabola.
C) Both variables are squared and have the same sign, but they aren't multiplied by the same number, so this is an ellipse.
D) Both variables are squared, and the squared terms have opposite signs, so this is an hyperbola.
If they give you an equation with variables on either side of the "equals" sign, rearrange the terms (on paper or in your head) to get the squared stuff together on one side. Then compare with the flow-chart above to find the type of equation you're looking at.
You may have noticed, in the table of "typical" shapes (above), that the graphs paralleled either the x-axis or the y-axis, and you may have wondered whether conics can ever be "slanted" with respect to the axes.
Can conic graphs be at angles to the axes?
As you can see below, yes, conics can have graphs that don't parallel the x- or y-axes, but instead go off at angles to the axes:
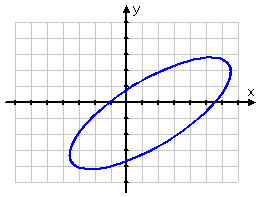
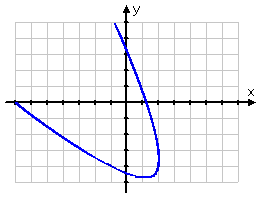
But the equations for the "slanty" conics get so much more messy that you can't deal with them until after trigonometry. If you wondered why the coefficients in the "general conic" equations, such as Ax2 + Cy2 + Dx + Ey + F = 0, skipped the letter B, it's because the B is the coefficient of the "xy" term that you can't handle until after you've taken trig.
You'll probably never have to deal with the "slanty" conics until calculus, when you may have to do "rotation of axes". Don't be in a rush. It's not a pretty topic.
Can a straight line be a conic?
Technically, yes. Think about the two nose-to-nose cones one uses for conics, and slice those cones so that the cut passes through the point where the two cones' tips touch. The curve created is just straight lines that pass along the outsides of the cones.
Once you have classified a conic, what can you do with it? The following lessons give some examples:
© 2024 Purplemath, Inc. All right reserved. Web Design by 