Introduction to Parabolas
Purplemath
What is a parabola?
A parabola is a particular type of geometrical curve which, algebraically, corresponds to a quadratic equation. In geometrical terms, the parabola corresponds to the edge of slice of an inverted cone; this slice is what is called the conic "section".
Content Continues Below
In physical terms, the circle is the line formed by looping a string around a stick stuck in the sand, sticking another stick in the other end of the looped thread, pulling the string taut with this stick, and pulling this stick around the first stick. An ellipse is formed by putting two sticks in the sand, looping a string around both of them (with that loop being long enough to be loose around the sticks), putting a third stick in the loop pulling out the slack, and pulling this stick around the two sticks in the ground.
How is a parabola constructed?
Affiliate
Advertisement
A parabola can be constructed with the help of a T-square and a rail. Rest the T-square on the rail. Put a pin on the board, above the rail. Put another pin in the top of the T-square. Pull the string taut along the vertical edge of the T-square. Slide the T-square from side to side, keeping the marker and string against the vertical edge. The resulting curve is a parabola.
(These physical drawings, called pin-and-string constructions, can be hard to picture in your head. If you'd like to watch these constructions, try this video. The parabola starts right at the one-minute mark.)
In algebra, dealing with parabolas usually means graphing quadratics or finding the max/min points (that is, the vertices) of parabolas for quadratic word problems. In the context of conics, however, there are some additional considerations.
What are the keywords for parabolas?
The keywords for parabolas are the vertex, the focus, the directrix, and the axis of symmetry. To form a parabola according to ancient Greek definitions, you would start with a straight line and a point off to one side; the line is called the directrix; the point is called the focus. The parabola is the curve formed from all the points (x, y) that are equidistant from the directrix and the focus.
The line perpendicular to the directrix and passing through the focus (that is, the line that splits the parabola up the middle) is called the axis of symmetry. The point on this axis which is exactly midway between the focus and the directrix is the vertex; the vertex is the point where the parabola changes direction.
Consider this "regular" (that is, an upright or an upside-down, but not sideways) parabola:
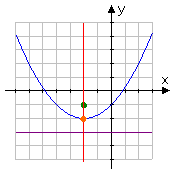
In the above picture, the parabola itself is drawn in blue. The focus (marked in green) is inside the parabola, the vertex (marked in orange) is at the turning point of the graph, the directrix (marked in purple) is the straight line on the other side of the vertex from the focus, and the axis of symmetry (marked in red) passes vertically through the focus and is perpendicular to the directrix.
You will almost always be dealing with vertical parabolas like the one above. But you might also (but only during the section on conics) have deal with horizontal ones like this:
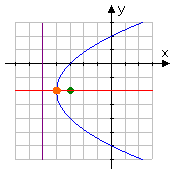
This is a sideways, or horizontal, parabola (in blue). On this graph, you can see the focus (marked in green) inside the parabola, the vertex (marked in orange) on the graph, the directrix (marked in purple) on the other side of the vertex from the focus, and the axis of symmetry (marked in red) passing through the focus and perpendicular to the directrix. The focus of a parabola is always inside the parabola; the vertex is always on the parabola; the directrix is always outside the parabola.
Content Continues Below
Where did the word parabola come from?
The name parabola is derived from a New Latin term that means something similar to compare or balance, and refers to the fact that the distance from the parabola to the focus is always equal to (that is, is always in balance with) the distance from the parabola to the directrix. In practical terms, you'll probably only need to know that the vertex is exactly midway between the directrix and the focus.
What is the basic physical property of parabolas?
A basic property of parabolas in real life is that any light, satellite signal, sound wave, etc, that enterw the parabola parallel to the axis of symmetry and hitting the inner surface of the parabolic bowl (like a satellite dish) will be reflected back to the focus. Parabolic dishes, such as bionic ears and radio telescopes, take advantage of this property to concentrate a signal onto a receiver.
What is the general form of a parabola's equation?
The general form of a parabola's equation is the quadratic that you're used to:
y = ax2 + bx + c
— unless the quadratic is sideways, in which case the equation will look something like this:
x = ay2 + by + c
The important difference in the two equations is in which variable is squared: for regular (that is, for vertical) parabolas, the x part is squared; for sideways (that is, for horizontal) parabolas, the y part is squared.
What is the vertex form of a parabola's equation?
The vertex form of a parabola — one with its vertex at the point (h, k) — is:
regular: y = a(x − h)2 + k
sideways: x = a(y − k)2 + h
The vertex form may also be expressed as:
regular: y − k = a(x − h)2
sideways: x − h = a(y − k)2
What is the conics form of a parabola's equation?
The conics form of the parabola equation (the one you'll find in advanced or older texts) is:
regular: 4p(y − k) = (x − h)2
sideways: 4p(x − h) = (y − k)2
Why do we use the letters h, k, and p in parabola equations?
Why (h, k) for the vertex, and p instead of a in the old-time conics formula? Dunno. And it isn't even true that "everybody" uses those letters. (Math StackExchange discussion, with link to archived AskDrMath article) So your guess is as good as mine (although, if you come across a source that seems authoritative, please do drop me a line).
What is the relationship between the vertex and geometrical forms of the parabola equation?
Affiliate
The important thing to notice, whether you're working with the vertex form or the geometrical form (that is, the conics form) of the parabola equation, is that the h always stays with the x part, that the k always stays with the y part, and that the p is always on the unsquared variable part.
In fact, the relationship between the vertex form of the equation and the conics form of the equation is nothing more than a rearrangement:
y = a(x − h)2 + k
y − k = a(x − h)2
(1/a)(y − k) = (x − h)2
4p(y − k) = (x − h)2
In other words, the value of 4p is actually the same as the value of 1/a; they're just two ways of saying the exact same thing. But this new variable p is one you'll need to be able to work with when you're doing parabolas in the context of conics: it represents the distance between the vertex and the focus, and is also the same as (that is, is also equal to) the distance between the vertex and the directrix; so 2p is then the distance between the focus and the directrix.
What is the relationship between the vertex and the general forms of the parabola equation?
The vertex form of a parabola's equation is converted into the general form by multiplying everything out and isolating the unsquared variable on one side of the "equals" sign, with the quadratic expression on the other side. The general form of a parabola's equation is converted into the vertex form by completing the square — or by using the following formula to get the value of h, being the x-coordinate of the vertex:
Then plug the value of h in for x in the parabola's general form, and simplify to get the value of y = k.
What are the rules of parabolas?
The rules for parabolas are:
- The vertex is always at the point (h, k; this is the point where the graphed curve turns around and starts heading back the way it came.
- Whether you're working with the leading coefficient a or the geometrical coefficient p (where p = 1/a):
- if the coefficient is positive, then the curve opens upwards (or, if sideways, to the right).
- if the coefficient is negative, then the curve opens downwards (or, if sideways, to the left).
- The axis of symmetry is the line that splits the parabola into two equal halves.
- If the parabola is vertical, then the axis of symmetry passes through the vertex and is the vertical line x = h.
- If the parabola is sideways, then the axis of symmetry passes through the vertex and is the horizontal line y = k.
- The focus will be the point p units from the vertex, and will be inside the parabola on the axis of symmetry
- The directrix will be the line p units from the vertex, and will be outside the parabola and perpendicular to the axis of symmetry.
How do you remember the rules for parabolas?
In my experience, the best way to learn and remember the rules for parabolas — and especially the relationships between the general, vertex, and geometrical forms, is to practice, practice, practice. Your brain will get bored enough (or frustrated enough) at having to look up the same stuff over and over again, and will start remembering the relationships out of pure laziness. At least, that's how *my* brain works.
URL: https://www.purplemath.com/modules/parabola.htm
You can use the Mathway widget below to practice finding the vertex. Try the entered exercise, or type in your own exercise. Then click the button and select "Find the Vertex Form" to compare your answer to Mathway's. (Or skip the widget, and continue to the next page.)
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()




