Extracting the Parabola's Info from its Equation
Purplemath
When you first start working with parabolas, the equations will almost always already be in vertex form which, depending on the parabola's orientation (vertical or sideways), will be one of the following:
y − k = a(x − h)2
x − h = a(y − k)2
Content Continues Below
The first thing you'll be doing is finding the vertex of a given parabola, plus maybe also its focus or directrix.
- State the vertex and focus of the parabola having the equation (y − 3)2 = 8(x − 5).
I can see that this is the conics, or geometrical, form of the parabola's equation. Remembering that the h always goes with the x and the k always goes with the y, I can see that the vertex is at the following point:
Advertisement
(h, k) = (5, 3)
Affiliate
The coefficient of the unsquared part is 4p; in this case, that gives me:
4p = 8
p = 2
Since the y part is squared and p is positive, then this is a sideways parabola that opens to the right. The focus is inside the parabola, so it has to be two units to the right of the vertex; that is, I'll need to add 2 to the x-coordinate of the vertex to get the focus. Then the focus is at:
(5 + 2, 3) = (7, 3)
So my hand-in answer is:
vertex: (5, 3)
focus: (7, 3)
- State the vertex, directrix, and intercepts of the parabola having the equation (x + 3)2 = −20(y − 1).
The temptation is to say that the vertex is at (3, 1), but that would be wrong. The conics form of the equation has subtraction inside the parentheses, so the (x + 3)2 is really (x − (−3))2, and the vertex is at (−3, 1).
The coefficient of the unsquared part is −20, and this is also the value of 4p, so p = −5. Since the x part is squared, this is a regular (that is, a vertical) parabola; and since the value of p is negative, then this parabola opens downward.
Since the directrix is on the outside of its parabola, and since this parabola is vertical and opening downward, then the directrix must be five units above the vertex. Since the y-value of the vertex is 1, then the directrix is at 1 + 5 = 6 = y.
To find the intercepts, we plug in zeroes in for our variables. (Note: While a given regular parabola will always eventually cross the y-axis, it might not cross the x-axis. For instance, if the vertex of this parabola had been below the x-axis, then the curve would never have crossed, and there would be no x-intercepts.)
For the x-intercepts, we plug zero in for y:
For the y-intercept, we plug zero in for x and solve:
Putting it all together, my hand-in answer is:
vertex: (−3, 1)
directrix: y = 6
intercepts:
Content Continues Below
- Graph x2 = 4y and state the vertex, focus, axis of symmetry, and directrix.
Once I divide through by 4, I can see that this is the same graphing that I've done in the past; the quadratic for this parabola is y = (1/4)x2. So I'll do the graph as usual, starting by plotting some points from a T-chart:
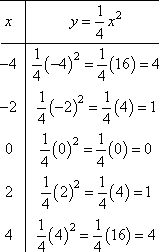
Here is my graph:
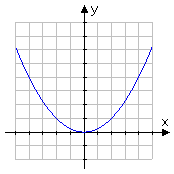
The vertex is obviously at the origin, but I need to show this algebraically by rearranging the given equation into the conics form:
x2 = 4y
(x − 0)2 = 4(y − 0)
Affiliate
This rearrangement shows that the vertex is at (h, k) = (0, 0). The axis of symmetry is the vertical line right through the vertex: x = 0. (I can always check my graph, if I'm not sure about this.) The focus is p units from the vertex. Since the focus is inside the parabola and since this is a right side up graph, the focus has to be above the vertex.
From the conics form of the equation, being x2 = 4y, I look at what's multiplied on the unsquared part and see that 4p = 4, so p = 1. Then the focus, being one unit above the vertex, is at (0, 1), and the directrix is the horizontal line one unit below the vertex, so its equation is y = −1.
Putting it all together with my graph above, my answer is:
vertex: (0, 0)
focus: (0, 1)
axis of symmetry: x = 0
directrix: y = −1
- Graph y2 + 10y + x + 25 = 0, and state the vertex, focus, axis of symmetry, and directrix.
Since the y is squared in this equation, rather than the x, then this is a sideways (or horizontal) parabola. To graph, I'll do my T-chart backwards, picking y-values first and then finding the corresponding x-values for x = −y2 − 10y − 25:
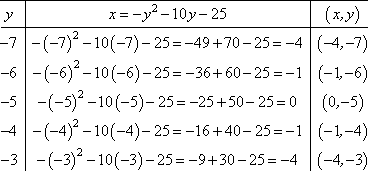
Then my graph looks like this:
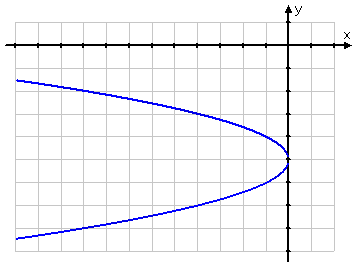
To convert the equation into conics form and find the exact vertex, etc, I'll need to complete the square. In this case, the squared side is already a perfect square, so:
y2 + 10y + 25 = −x
(y + 5)2 = −1(x − 0)
This tells me that 4p = −1, so p = −1/4. Since the parabola opens to the left, then the focus is 1/4 units to the left of the vertex. I can see from the equation above that the vertex is at (h, k) = (0, −5), so then the focus must be at (−1/4, −5). The parabola is sideways, so the axis of symmetry is, too. The directrix, being perpendicular to the axis of symmetry, is then vertical, and is 1/4 units to the right of the vertex. Putting this all together, I get:
vertex: (0, −5)
focus: (−1/4, −5)
axis of symmetry: y = −5
directrix: x = 1/4
- Find the vertex and focus of y2 + 6y + 12x − 15 = 0
The y part is squared, so this is a sideways parabola. I'll get the y stuff by itself on one side of the equation, and then complete the square to convert this to conics form.
y2 + 6y − 15 = −12x
y2 + 6y + 9 − 15 = −12x + 9
(y + 3)2 − 15 = −12x + 9
(y + 3)2 = −12x + 9 + 15 = −12x + 24
(y + 3)2 = −12(x − 2)
(y − (−3))2 = 4(−3)(x − 2)
Then the vertex is at (h, k) = (2, −3) and the value of p is −3. Since y is squared and p is negative, then this is a sideways parabola that opens to the left. This puts the focus 3 units to the left of the vertex.
vertex: (2, −3)
focus: (−1, −3)
URL: https://www.purplemath.com/modules/parabola2.htm
You can use the Mathway widget below to practice extracting a parabola's information from its equation. Try the entered exercise, or type in your own exercise. Then click the button and select the option matching what you're looking for, to compare your answer to Mathway's. (Or skip the widget, and continue on to the next page.)
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()




