Graphing Quadratic Functions: Introduction

Index of lessons
Print this page (print-friendly version) | Find local tutors

Graphing Quadratic Functions (page 1 of 4)

Sections: Introduction, The meaning of the leading coefficient / The vertex, Examples

The general technique for graphing quadratics is the same as for graphing linear equations. However, since quadratics graph as curvy lines (called "parabolas"), rather than the straight lines generated by linear equations, there are some additional considerations.

The most basic quadratic is y = x². When you graphed straight lines, you only needed two points to graph your line, though you generally plotted three or more points just to be on the safe side. However, three points will almost certainly not be enough points for graphing a quadratic, at least not until you are very experienced. For example, suppose a student computes these three points:

table of values: (0,0), (1,1), (2,4)

Then, based only on his experience with linear graphs, he tries to put a straight line through the points.

incorrect graph

Quadratics graph as curves, not as striaght lines like this.

He got the graph wrong. You, on the other hand, are more careful.

You find many points:

table of values: (-3,9), (-2,4), (-1,1), (0,0), (1,1), (2,4), (3,9), (4,16)

That last point has a rather large y-value, so you decide that you won't bother drawing your graph large enough to plot it.

But you plot all the other points:

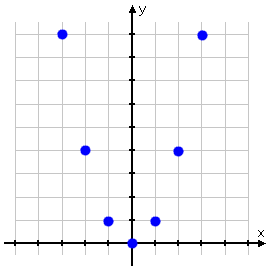
plotted points

Even if you'd forgotten that quadratics graph as curvy parabolas, these points will remind you of this fact.

You draw a nicely smooth curving line passing neatly through the plotted points:

correct graph of y = x²

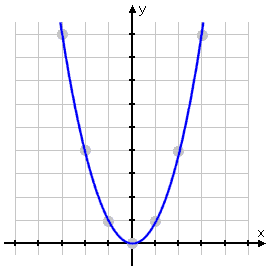
graph of y = x^2

Unlike the careless student, you just got the graph right.

Some students will plot the points correctly, but will then connect the points with straight line segments, like this:

incorrect "segment" graph

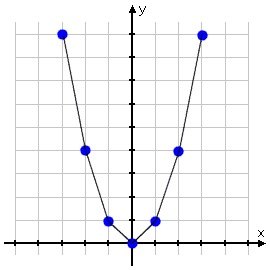
Parabolas are smooth curves, not jointed segments like this.

This is not correct. You do still need a ruler for doing your graphing, but only for drawing the axes, not for drawing the parabolas. Parabolas graph as smoothly curved lines, not as jointed segments.

Top | 1 | 2 | 3 | 4 | Return to Index Next >>

Cite this article as:

Stapel, Elizabeth. "Graphing Quadratic Functions: Introduction." Purplemath. Available from
https://www.purplemath.com/modules/grphquad.htm. Accessed

MathHelp.com Courses

Copyright © 2021 Elizabeth Stapel \| About \| Terms of Use \| Linking \| Site Licensing		Contact Us