An Introduction to Hyperbolas
Purplemath
Hyperbolas don't come up much — at least not that I've noticed — in other math classes, but if you're covering conics in your current class, then you'll need to know their basics.
These basics include hyperbola's keywords and what they mean, and how to relate equations and info such as the hyperbola's center and foci.
Content Continues Below
What is an hyperbola?
An hyperbola is one of the conic sections. Its equation is similar to that of an ellipse, but with a subtraction sign in the middle. The graph of an hyperbola looks nothing like an ellipse.
What does an hyperbola look like?
An hyperbola looks sort of like two mirrored parabolas, with the two halves being called "branches". Like an ellipse, an hyperbola has two foci and two vertices; unlike an ellipse, the foci in an hyperbola are further from the hyperbola's center than are its vertices, as displayed below:
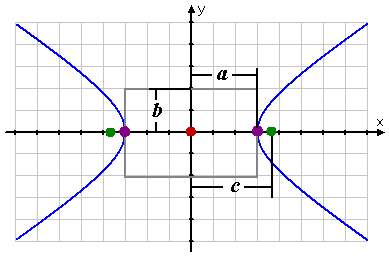
The hyperbola is centered on a point (h, k), which is the center of the hyperbola. (In the above grapic, the center happens to be the origin.)
Affiliate
Advertisement
The point on each branch closest to the center is that branch's vertex The vertices are some fixed distance a from the center.
The line going from one vertex, through the center, and ending at the other vertex is called the transverse (or major) axis.
As with ellipses, there is a relationship between a, b, and c, and, as with ellipses, the computations are long and painful. So trust me that, for hyperbolas (where a < c), the relationship is c2 − a2 = b2 or, which means the same thing:
c2 = b2 + a2
...where a2 and b2 are the denominators of the two fractions in the conics form of the hyperbola equation.
(Yes, these are the same letters as are used in the Pythagorean Theorem. Yes, the Pythagorean Theorem is used to prove this relationship. No, this is not the same thing as the Pythagorean Theorem. Yes, this is very confusing. Just memorize it, and move on.)
The foci of an hyperbola are inside the curve of each branch, and each focus is located some fixed distance c from the center. (This means that a < c for hyperbolas.) This length xis called the focal parameter.
The values of a and c will vary from one hyperbola to another, but they will be fixed values for any one particular hyperbola.
For any point on an ellipse, the sum of the distances from that point to each of the foci is some fixed value; for any point on an hyperbola, it's the difference of the distances from the two foci that is fixed. Looking at the graph above and letting "the point" be one of the vertices, this fixed distance must be (the distance to the further focus) less (the distance to the nearer focus), or (a + c) − (c − a) = 2a.
This fixed-difference property can used for determining locations. For instance, if two beacons are placed in known and fixed positions, the difference in the times at which their signals are received by, say, a ship at sea can tell the crew where they are.
Content Continues Below
What is the equation of an hyperbola?
The equation for an hyperbola comes in two versions, depending upon how the hyperbola splits into two branches. These two versions are:
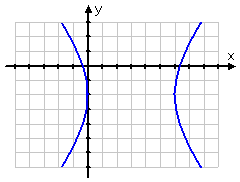
When the transverse axis is horizontal (in other words, when the branches are side by side), then the a2 goes with the x part of the hyperbola's equation, and the y part is subtracted, as shown below:
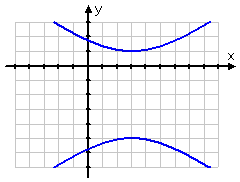
When the transverse axis is vertical (in other words, when the branches are above and below each other), then the a2 goes with the y part of the hyperbola's equation, and the x part is subtracted, as shown below:
These equations can be presented as fully multiplied-out and simplified. For example, we can take the following hyperbola's conics (or vertex) form:
...and multiply it out:
Affiliate
Note: When in vertex format, an hyperbola's equation is always "=1". The above multiplied-out equation might be referred to, in your textbook, as the general or standard form of the equation. I think of it as the unhelpful form.
The value of b gives the height of the "fundamental box" for the hyperbola (marked in grey in the graphic below), and 2b is the length of the conjugate (or minor) axis. (This information doesn't help you graph hyperbolas, though. The value of b is pretty much used — in graphing — only to find the value of c.)

For reasons you'll learn in calculus, the graph of an hyperbola gets fairly flat and straight when it gets far away from its center. If you zoom out from the graph, it will look very much like an X, with maybe a little curviness near the middle. These nearly straight parts get very close to what are called the asymptotes of the hyperbola.
For an hyperbola centered at (h, k) and having fixed values a and b, the asymptotes are given by the following equations, depending on the hyperbola's orientation:
hyperbola with side-by-side branches:
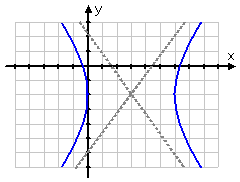
side-by-side hyperbola's asymptotes' equation:
hyperbola with top and bottom branches:
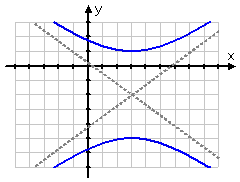
top and bottom hyperbola's asymptotes' equation:
Note that the only difference in the asymptote equations above is in the slopes of the straight lines. If a2 is the denominator for the x part of the hyperbola's equation, then a is still in the denominator in the slope of the asymptotes' equations; if a2 goes with the y part of the hyperbola's equation, then a goes in the numerator of the slope in the asymptotes' equations.
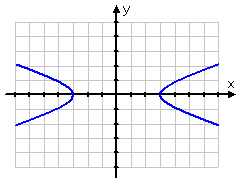
Hyperbolas can be fairly "straight" or else pretty "bendy", depending upon something called their eccentricity:
hyperbola with an eccentricity of about 1.05:
hyperbola with an eccentricity of about 7.6:
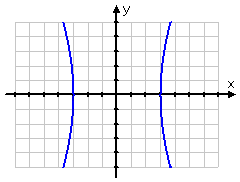
The eccentricity e is the measure of the amount of curvature in the hyperbola's branches, where e = c/a. Since the foci are further from the center of an hyperbola than are the vertices (so c > a for hyperbolas), then e > 1. Bigger values of e correspond to the straighter types of hyperbolas, while values closer to 1 correspond to hyperbolas whose graphs curve quickly away from their centers.
What is the meaning of the word "hyperbola"?
The term hyperbola comes to us from Greek roots that indicate excessiveness, but the curve wasn't given this name until the mid-1600's. I suspect this name was chosen because the eccentricity of an hyperbola is greater than 1, and can be as large as you like. The other conics have eccentricities between 0 and 1, so the hyperbola's eccentricity, by comparison, is a bit excessive... I guess.
Note: The e that stands for eccentricity is different for different hyperbolas. In particular, this e is not fixed, and is not the same as the number e ≈ 2.7. Don't confuse the two!
URL: https://www.purplemath.com/modules/hyperbola.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()




