Conics: Hyperbolas: Finding Information
     From the Equation(page 2 of 3)

Sections: Introduction, Finding information from the equation, Finding the equation from information

• Find the center, vertices, foci, eccentricity, and asymptotes of the hyperbola with the given equation, and sketch:  

Since the y part of the equation is added, then the center, foci, and vertices will be above and below the center (on a line paralleling the y-axis), rather than side by side.

Looking at the denominators, I see that a² = 25 and b² = 144, so a = 5 and b = 12. The equation c² – a² = b² tells me that c² = 144 + 25 = 169, so c = 13, and the eccentricity is e = 13/5. Since x² = (x – 0)² and y² = (y – 0)², then the center is at (h, k) = (0, 0). The vertices and foci are above and below the center, so the foci are at (0, –13) and (0, 13), and the vertices are at (0, 5) and (0, –5).

Because the y part of the equation is dominant (being added, not subtracted), then the slope of the asymptotes has the a on top, so the slopes will be m = ± 5/12. To graph, I start with the center, and draw the asymptotes through it, using dashed lines:
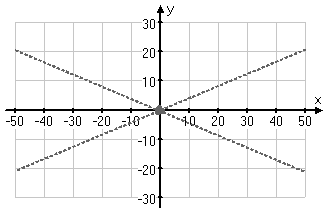
Then I draw in the vertices, and rough in the graph, rotating the paper as necessary and "eye-balling" for smoothness:
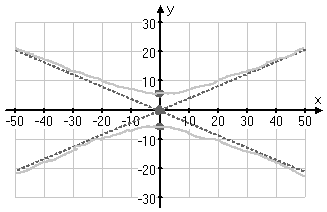
Then I draw in the final graph as a neat, smooth, heavier line:

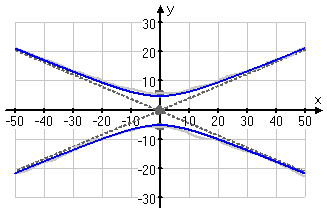
And the rest of my answer is:

center (0, 0), vertices (0, –5) and (0, 5), foci (0, –13) and (0, 13),
eccentricity , and asymptotes

• Give the center, vertices, foci, and asymptotes for the hyperbola
  with equation:   

Since the x part is added, then a² = 16 and b² = 9, so a = 4 and b = 3. Also, this hyperbola's foci and vertices are to the left and right of the center, on a horizontal line paralleling the x-axis.

From the equation, clearly the center is at (h, k) = (–3, 2). Since the vertices are a = 4 units to either side, then they are at (–7, 2) and at (1, 2). The equation c² – a² = b² gives me c² = 9 + 16 = 25, so c = 5, and the foci, being 5 units to either side of the center, must be at (–8, 2) and (2, 2). Copyright © Elizabeth Stapel 2010-2011 All Rights Reserved

Since the a² went with the x part of the equation, then a is in the denominator of the slopes of the asymptotes, giving me m = ± 3/4. Keeping in mind that the asymptotes go through the center of the hyperbola, the asymptes are then given by the straight-line equations  y – 2 = ± (3/4)(x + 3).

center (–3, 2), vertices (–7, 2) and (1, 2), foci (–8, 2) and (2, 2),
and asymptotes

• Find the center, vertices, and asymptotes of the hyperbola with equation
  4x² – 5y² + 40x – 30y – 45 = 0.

To find the information I need, I'll first have to convert this equation to "conics" form by completing the square.

4x² + 40x – 5y² – 30y = 45
4(x² + 10x        ) – 5(y² + 6y       ) = 45 + 4(   ) – 5(  )
4(x² + 10x + 25) – 5(y² + 6y + 9) = 45 + 4(25) – 5(9)
4(x + 5)² – 5(y + 3)² = 45 + 100 – 45





Then the center is at (h, k) = (–5, –3). Since the x part of the equation is added, then the center, foci, and vertices lie on a horizontal line paralleling the x-axis; a² = 25 and b² = 20, so a = 5 and b = 2sqrt[5]. The equation a² + b² = c² gives me c² = 25 + 20 = 45, so c = sqrt[45] = 3sqrt[5]. The slopes of the two asymptotes will be m = ± (2/5)sqrt[5]. Then my complete answer is:

center (–5, –3), vertices (–10, –3) and (0, –3),

foci  and ,

and asymptotes

If I had needed to graph this hyperbola, I'd have used a decimal approximation of ± 0.89442719... for the slope, but would have rounded the value to something reasonable like m = ± 0.9.

<< Previous  Top  |  1 | 2 | 3  |  Return to Index  Next >>

  Copyright © 2010-2012  Elizabeth Stapel   |   About   |   Terms of Use

 Feedback   |   Error?