Multiplying Simple Polynomials
Purplemath
Just as we can multiply numbers, so also we can multiply polynomials. And just as some numerical multiplication is easier than others, so it is with polynomials.
The simplest multiplication involving polynomials is where we're taking a number through a set of parentheses.
Content Continues Below
- Simplify the following: −5 (2x2)
All I have to do here is multiply the −5 by the 2, while carrying the x2 along for the ride:
−5 (2x2)
(−5)(2)(x2)
−10x2
We can also multiply a number through a parenthetical which contains more than one term. In such a case, the number gets multiplied onto each/all of the terms inside.
- Simplify the following: 2 (3x + 1)
Advertisement
I have a number (being the 2 to the left of, or in front of, the parenthetical) that I need to take through (or, using the technical terms, "distribute over") the expression inside the parentheses (being the 3x + 1). I'll show every step:
2 (3x + 1)
2 (3x) + 2 (+1)
(2)(3)(x) + (2)(1)
(6)(x) + 2
6x + 2
At this point, I'm left with two un-like terms, so I cannot combine or simplify any further. My answer is:
6x + 2
You may already have seen this sort of computation when you learned about simplifying with parentheses.
(You likely won't need to use so many steps as I did above, at least not once you're comfortable with the process, and your instructor almost certainly won't be expecting this much. I'm being overly complete in this lesson in hopes that, by the time you're done, you will be sure of what's going on and will feel comfortable with the process.)
Moving up in complexity, we can multiply two single-term polynomials (called "monomials").
- Simplify (5x2)(−2x3)
Affiliate
I've already done this type of multiplication when I was first learning about exponents, negative numbers, and variables. I'll apply the rules that I already know, being careful to carry the "minus" sign along with its number (being the 2):
(5x2)(−2x3)
(5)(x2)(−2)(x3)
(5)(−2)(x2)(x3)
(−10)(x2+3)
−10x5
I can't simplify any further, so I'm done. My answer is:
−10x5
Usually (and in contrast to the exercise just completed), a monomial that's going to be taken through a parenthetical doesn't have parentheses around it. Instead, the multiplication is indicated simply by the "juxtaposition" of the monomial with (that is, by putting the monomial right next to) the parenthetical expression. This is called "multiplication by juxtaposition", and it looks like this:
- Simplify −3x (1 − x)
I'll need to be careful with my "minus" signs.
−3x (1 − x)
−3x(1) + (−3x)(−x)
−3x + (+3)(x)(+x)
−3x + 3x2
A monomial can be multiplied through longer polynomials, too.
- Simplify −3x(4x2 − x + 10)
To do this multiplication, I have to distribute the −3x through the parentheses:
−3x(4x2 − x + 10)
−3x(4x2) + (−3x)(−x) + (−3x)(+10)
(−3)(4)(x)(x2) + (+3)(x)(+x) + (−3)(10)(x)
(−3)(4)(x)(x2) + (+3)(x)(+x)
+ (−3)(10)(x)
(−12)(x1+2) + (3)(x1+1) + (−30)(x)
−12x3 + 3x2 − 30x
Content Continues Below
The next step up in complexity is the multiplication of one two-term polynomial by another two-term polynomial (that is, one binomial by another binomial). This is the simplest of the "multi-term times multi-term" cases. There are actually three ways to do this. Since this is one of the most common polynomial multiplications that you likely will be doing, I'll spend a fair amount of time on this.
-
Simplify (x + 3)(x + 2)
The first way I can do this multiplication is by working "horizontally" (this is the method that I was taught back in high school). Doing so, I will have to distribute twice, taking each of the terms in the first parentheses "through" each of the terms in the second parentheses.
(x + 3)(x + 2)
(x + 3)(x) + (x + 3)(+2)
x(x) + 3(x) + x(+2) + 3(+2)
x2 + 3x + 2x + 6
x2 + 5x + 6
This horizontal multiplication, while mathematically valid, is probably the most difficult and error-prone way to do this multiplication. The "vertical" method is much simpler. Think back to when you were first learning about multiplication. When you did small numbers, it was simplest to work horizontally:
3 × 4 = 12
Affiliate
But when you got to larger numbers, you stacked the numbers vertically and, working from right to left, took one digit at a time from the lower number and multiplied it, right to left, across the top number. For each digit in the lower number (first the ones digit, then the tens digits, then the hundreds digits, and so forth), you formed a new row underneath, stepping the rows off to the left as you worked from right-most digit to left-most digit in the lower number. Then you added down.
For instance, you would probably not want to try to multiply 121 by 32 horizontally, but it's easy when you do it vertically:
You can multiply polynomials in this same manner, so here's the same exercise as above, but done "vertically" this time:
-
Simplify (x + 3)(x + 2)
I need to be sure to do my work very neatly. First, I'll set up the multiplication:
...and then I'll multiply:
Multiply the bottom +2 by the top +3, and carry down the +6:
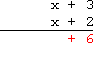
Multiply the bottom +2 by the top x, and carry down the +2x:
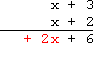
Multiply the bottom x by the top +3, and carry down the +3x:
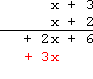
Multiply the bottom x by the top x, and carry down the x2:
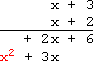
Draw a horizontal line below the two new rows:
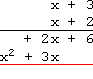
Carry the x2 down to the bottom:
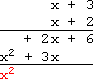
Add the +2x and the +3x, bringing down a +5x:
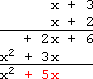
Carry the +6 down to the bottom:
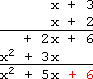
The completed vertical multiplication:
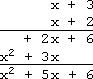
As you can see, I got the same answer working vertically as when I multiplied horizontally:
x2 + 5x + 6
But the vertical method kept track of the signs, etc, for me, which made the process much less painful.
URL: https://www.purplemath.com/modules/polymult.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()