Multiplying General Polynomials
Purplemath
Sometimes (such as in calculus) you will need to multiply one multi-term polynomial by another multi-term polynomial. You can do this horizontally if you want, but there is so much room for error that I always switch over to vertical multiplication once the polynomials get past two terms in length (and usually for the binomials, too). For bigger multiplications, vertical multiplication is usually faster, and is much more likely to give you a correct answer.
Content Continues Below
-
Simplify (4x2 − 4x − 7)(x + 3)
Here's what the multiplication looks like when it's done horizontally:
(4x2 − 4x − 7)(x + 3)
(4x2 − 4x − 7)(x) + (4x2 − 4x − 7)(3)
4x2(x) − 4x(x) − 7(x) + 4x2(3) − 4x(3) − 7(3)
4x3 − 4x2 − 7x + 12x2 − 12x − 21
4x3 − 4x2 + 12x2 − 7x − 12x − 21
4x3 + 8x2 − 19x − 21
That was painful! Now I'll do it vertically:
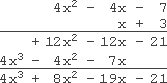
That was a lot easier! But, by either method, the answer is the same:
4x3 + 8x2 − 19x − 21
-
Simplify (x + 2)(x3 + 3x2 + 4x − 17)
I'm just going to do this one vertically; horizontally is too much trouble.
Note that, since order doesn't matter for multiplication, I can still put the "x + 2" polynomial on the bottom for the vertical multiplication, just as I always put the smaller number on the bottom when I was doing regular vertical multiplication with just plain numbers back in grammar school.
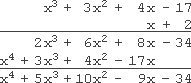
x4 + 5x3 + 10x2 − 9x − 34
Content Continues Below
-
Simplify (3x2 − 9x + 5)(2x2 + 4x − 7)
I'll take my time, and do my work neatly:
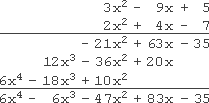
6x4 − 6x3 − 47x2 + 83x − 35
-
Simplify (x3 + 2x2 + 4)(2x3 + x + 1)
First off, I notice that terms of these polynomials have some power (that is, degree) "gaps".
Advertisement
Affiliate
The first polynomial has an x3 term, an x2 term, and a constant term, but no x term; and the second polynomial has an x3 term, an x term, and a constant term, but no x2 term. When I do the vertical multiplication, I will need to leave spaces in my set-up, corresponding to the "gaps" in the degrees of the polynomials' terms, because I will almost certainly need the space.
(This is similar to using zeroes as "place holders" in regular numbers. You might have a thousands digit of 3, a hundreds digit of 2, and a units digit of 5, so you'd put a 0 in for the tens digits, creating the number 3,205.)
Here's what that looks like:
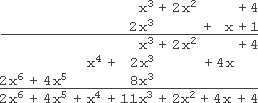
See how I needed the gaps? See how it helped that I had everything lined up according to the term's degree? If I hadn't left gaps when writing out my original factors, my terms could easily have become misaligned in the rows below. By taking the time to write things out explicitly neatly, I saved myself from many needless difficulties.
My answer is:
2x6 + 4x5 + x4 + 11x3 + 2x2 + 4x + 4
Affiliate
I did have one professor who could just look at huge polynomial products, and somehow keep all the terms straight while he did the multiplications and additions in his head. He'd write down the terms one-by-one, starting from the highest degree to the lowest, going straight from the original product to the final answer. He seriously freaked us all out!
While you may aspire to such proficiency, don't reject the tool of vertical multiplication, at least when you're getting started. Don't try to freak out your classmates until you're really good at using the regular methods.
You can use the Mathway widget below to practice multiplying general polynomials. Try the entered exercise, or type in your own exercise. Then click the button and select "Multiply" to compare your answer to Mathway's.
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
URL: https://www.purplemath.com/modules/polymult3.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()