"Solving" Quadratic Equations by Graphing
Purplemath
To be honest, solving "by graphing" is a somewhat bogus topic. The basic idea behind solving by graphing is that, since the (real-number) solutions to any equation (quadratic equations included) are the x-intercepts of that equation, we can look at the x-intercepts of the graph to find the solutions to the corresponding equation. However, there are difficulties with "solving" this way.
When we graph a straight line such as "y = 2x + 3", we can find the x-intercept (to a certain degree of accuracy) by drawing a really neat axis system, plotting a couple points, grabbing our ruler, and drawing a nice straight line, and reading the (approximate) answer from the graph with a fair degree of confidence.
Content Continues Below
However, the only way to know we have the accurate x-intercept, and thus the solution, is to use the algebra, setting the line equation equal to zero, and solving:
0 = 2x + 3
−3 = 2x
−1.5 = x
Advertisement
If the linear equation were something like y = 47x − 103, clearly we'll have great difficulty in guessing the solution from the graph. We might guess that the x-intercept is near x = 2 but, while close, this won't be quite right. Algebra would be the only sure solution method.
A quadratic function is messier than a straight line; it graphs as a wiggly parabola. If we plot a few non-x-intercept points and then draw a curvy line through them, how do we know if we got the x-intercepts even close to being correct? We don't. The only way we can be sure of our x-intercepts is to set the quadratic equal to zero and solve.
Affiliate
But the whole point of "solving by graphing" is that they don't want us to do the (exact) algebra; they want us to guess from the pretty pictures.
So "solving by graphing" tends to be neither "solving" nor "graphing". In a typical exercise, you won't actually graph anything, and you won't actually do any of the solving. Instead, you are told to guess numbers off a printed graph. Or else, if "using technology", you're told to punch some buttons on your graphing calculator and look at the pretty picture; and then you're told to punch some other buttons so the software can compute the intercepts.
My guess is that the educators are trying to help you see the connection between x-intercepts of graphs and solutions of equations. But the concept tends to get lost in all the button-pushing.
Okay, enough of my ranting.
Affiliate
To solve by graphing, the book may give us a very neat graph, probably with at least a few points labelled. The book will ask us to state the points on the graph which represent solutions. Otherwise, it will give us a quadratic, and we will be using our graphing calculator to find the answer. Since different calculator models have different key-sequences, I cannot give instruction on how to "use technology" to find the answers; you'll need to consult the owner's manual for whatever calculator you're using (or the "Help" file for whatever spreadsheet or other software you're using). I will only give a couple examples of how to solve from a picture that is given to you.
-
Solve x2 − 8x + 15 = 0 by using the following graph.
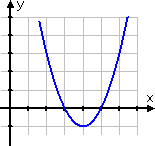
The equation they've given me to solve is:
0 = x2 − 8x + 15
The picture they've given me shows the graph of the related quadratic function:
y = x2 − 8x + 15
The x-intercepts of the graph of the function correspond to where y = 0. The point here is that I need to look at the picture (hoping that the points really do cross at whole numbers, as it appears), and read the x-intercepts of the graph (and hence the solutions to the equation) from the picture.
The graph appears to cross the x-axis at x = 3 and at x = 5 I have to assume that the graph is accurate, and that what looks like a whole-number value actually is one. So my answer is:
x = 3, 5
Since they provided the quadratic equation in the above exercise, I can check my solution by using algebra. The given quadratic factors, which gives me:
(x − 3)(x − 5) = 0
x − 3 = 0, x − 5 = 0
x = 3, 5
Now I know that the solutions are whole-number values. The graph can be suggestive of the solutions, but only the algebra is sure and exact.
Content Continues Below
-
Solve from the following graph.
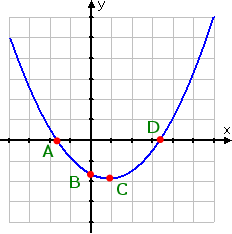
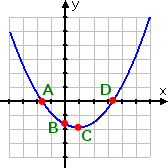
A , B , C , D
For this picture, they labelled a bunch of points. Partly, this was to be helpful, because the x-intercepts are messy, so I could not have guessed their values without the labels. But mostly this was in hopes of confusing me, in case I had forgotten that only the x-intercepts, not the vertices or y-intercepts, correspond to "solutions".
Point B is the y-intercept (because x = 0 for this point), so I can ignore this point. Point C appears to be the vertex, so I can ignore this point, also. Points A and D are on the x-axis (because y = 0 for these points). So I can assume that the x-values of these graphed points give me the solution values for the related quadratic equation.
Because they provided the equation in addition to the graph of the related function, it is possible to check the answer by using algebra. But the intended point here was to confirm that the student knows which points are the x-intercepts, and knows that these intercepts on the graph are the solutions to the related equation.
-
Find the solutions to the quadratic equation from the following graph:
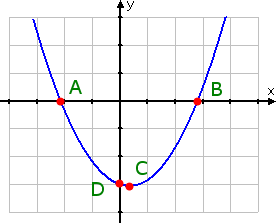
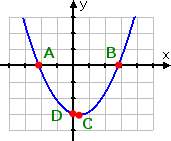
A = (−2.1429, 0), B = (2.8, 0), C = (0.3286, −3.0540), D = (0, −3)
They haven't given me a quadratic equation to solve, so I can't check my work algebraically. They have only given me the picture of a parabola created by the related quadratic function, from which I am supposed to approximate the x-intercepts, which really is a different question. But I know what they mean.
I can ignore the point which is probably the vertex (Point C). I can ignore the point which is the y-intercept (Point D). So I'll pay attention only to the x-intercepts, being those points where y is equal to zero. So my answer is:
x = −2,1429, 2.8
Solving quadratics by graphing is silly in terms of "real life", and requires that the solutions be the simple factoring-type solutions such as "x = 3", rather than something like "x = −4 + sqrt(7)". In other words, they either have to "give" you the answers (b labelling the graph), or they have to ask you for solutions that you could have found easily by factoring.
Affiliate
About the only thing you can gain from this topic is reinforcing your understanding of the connection between solutions of equations and x-intercepts of graphs of functions; that is, the fact that the solutions to "(some polynomial) equals (zero)" correspond to the x-intercepts of the graph of "y equals (that same polynomial)". If you come away with an understanding of that concept, then you will know when best to use your graphing calculator or other graphing software to help you solve general polynomials; namely, when they aren't factorable. And you'll understand how to make initial guesses and approximations to solutions by looking at the graph, knowledge which can be very helpful in later classes, when you may be working with software to find approximate "numerical" solutions.
But in practice, given a quadratic equation to solve in your algebra class, you should not start by drawing a graph. Which raises the question: For any given quadratic, which method should one use to solve it?
URL: https://www.purplemath.com/modules/solvquad5.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()