Solving Linear Equations w/ Parentheses
Purplemath
In this lesson, we'll first practice solving linear equations which contain parentheticals. Solving these will involve multiplying through and simplifying, before doing the actual solution process. If you're not comfortable with parentheses, study up first. Then come back here.
Then we'll look at the two weird kinds of solutions: "no solution", and the solution that is "all x". The solution process ends in nonsense in the former case, and in a trivially-true statement in the latter. Because students don't encounter these types of solutions often, they're easy to forget, and thus easy to confuse. But I'd bet good money that there will be at least one of these equations on the next test, with another one probably on the final. So study up, and make a note now to review "no solution" equations and "all-x solution" equations before the next exam.
Content Continues Below
Once you've learned the basics of solving linear equations, your textbook and instructor will start throwing exercises at you that involve parentheticals which usually need first to be simplified (or "expanded", which means that you've multiplied through and then simplified the result).
-
Solve 9 = 3(5x − 2)
First, I have to multiply through the parentheses on the right-hand side. Then I can proceed in the usual way:
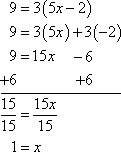
Then my solution is:
x = 1
-
Solve 6x − (3x + 8) = 16
I'll simplify on the left-hand side first; then I'll solve in the usual way. I want to be careful when I'm taking negatives through parentheses. If I'm having trouble keeping track of the "minus" signs, I'll put a "1" in front of the parentheses.
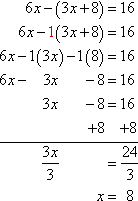
Then my solution is:
x = 8
-
Solve 7(5x − 2) = 6(6x − 1)
This equation has parentheticals on both sides of the equation. I have to be sure to take the 7 and the 6 all the way through their respective parentheses.
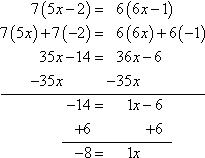
After I'd simplified either side, I moved the smaller of the two variable terms (being the "35x" on the left-hand side) to ensure that my resulting variable term had no "minus" sign on it. This isn't a "rule", but it certainly does make my life easier. And my final answer is:
x = −8
For equations with parentheticals, take your time and write out all of your steps, like I did above. Don't try to do everything in your head.
Content Continues Below
-
Solve 3(x − 2) = 6
First, I need to multiply through on the left-hand side, taking the 3 through the—
Wait a minute... For this equation, I can actually get rid of the 3 by dividing through, because the 6 on the right-hand side is divisible by 3. I don't actually need to distribute for this particular equation. Instead:
3(x - 2) = 6
-------- -
3 3
x - 2 = 2
+2 +2
----------
x = 4
Then my solution is:
x = 4
If I hadn't noticed that I could start by dividing through, I still would have gotten the right answer, eventually. But if it's possible to divide through, giving myself smaller numbers to work with, I do like to take advantage of that. This simplification doesn't occur often, but try not to be blind to it, the few times that it does pop up.
-
Solve 13 − (2x + 2) = 2(x + 2) + 3x
I'll start by multiplying through on each of the parentheticals (being a "minus" sign on the left, and a 2 on the right). Then I'll combine like terms, simplify, and solve:
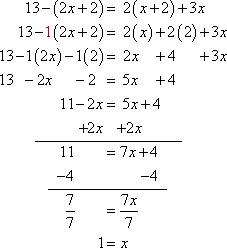
Then my answer is:
x = 1
Affiliate
Advertisement
Don't forget: There is never any reason to be unsure of your solution to a linear equation, because you can always check your answer. The meaning of the solution value is that it is the x-value that makes the equation true. So, to check your answer, you plug your solution value back into the original equation, and you make sure that the equation "works" with that value. For instance, in the last exercise above, my solution was x = 1. To check my solution, I'll plug my value into the left-hand side (LHS) and right-hand side (RHS) of the original equation, and make sure that both sides evaluate to the same number.
13 − (2x + 2) = 2(x + 2) + 3x
LHS: 13 − (2[1] + 2)
= 13 − (2 + 2) = 13 − 4 = 9
RHS: 2([1] + 2) + 3[1]
= 2(3) + 3 = 6 + 3 = 9
The two sides of the equation evaluate to the same value, so the solution "checks", and I now know that my answer is correct
By the way, if possible, you should try to check your answers when you take tests. Once you've completed all the questions (assuming you've got some time left over), go back and plug your solutions back into the original question. If your solution to a given question "checks", then you know you got that question right. If it doesn't check, then you have the chance to correct your mistake before you hand in your test.
You may need to solve linear equations with nested parentheses, too.
-
Solve 2[3x + 4(3 − x)] = 3(5 − 4x) − 11
Before I can solve, I'll need to simplify. I'll simplify the left-hand side first:
2[3x + 4(3 − x)]
2[3x + 4(3) + 4(−x)]
2[3x + 12 − 4x]
2[12 − x]
24 − 2x
Then I'll simplify the right-hand side:
3(5 − 4x) − 11
3(5) + 3(−4x) − 11
15 − 12x − 11
4 − 12x
Now that I have simplified either side of the equation, I can proceed to solving.
24 - 2x = 4 - 12x
+12x +12x
-------------------
24 + 10x = 4
-24 -24
--------------
10x = -20
--- ---
10 10
x = -2
So my final answer is:
x = −2
Affiliate
-
Solve 3[x − 2(3x − 4)] + 15 = 5 − [2x − (3 + x)] − 11
My first step will be to simplify each side of this equation, working from the inside out. I'll start on the left-hand side:
3[x − 2(3x − 4)] + 15
3[x − 6x + 8] + 15
3[−5x + 8] + 15
−15x + 24 + 15
−15x + 39
Then I'll simplify the right-hand side:
5 − [2x − (3 + x)] − 11
5 − [2x − 3 − x] − 11
5 − [x − 3] − 11
5 − x + 3 − 11
−x − 3
With each side simplified, I can proceed to solving. My simplified equation is:
−15x + 39 = −x − 3
I'll move the smaller variable term (being the −15x on the left-hand side), and then move the numbers around to finish the solution.
-15x + 39 = -x - 3
+15x +15x
-------------------
39 = 14x - 3
+3 +3
------------
42 = 14x
-- ---
14 14
3 = x
x = 3
You can use the Mathway widget below to practice solving linear equations with nested parentheses. Try the entered exercise, or type in your own exercise. Then click the button and select "Solve for x" to compare your answer to Mathway's. (Or skip the widget, and proceed to the next page.)
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
URL: https://www.purplemath.com/modules/solvelin4.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()



