Solving Linear Equations w/ Zero Soln's, No Soln, and "All-x" Soln's
Purplemath
There are three solution types that can cause confusion. We'll look at one example of each, and I'll explain the differences. Then we'll work on a mixture of equation type, so that you can become more comfortable in telling the solution types apart.
-
Solve 5 − (3x + 4) = 1
To solve this equation, I first need to simplify the left-hand side by taking the "minus" through the parenthetical, and combining "like" terms:
Content Continues Below
5 − (3x + 4)
5 − 1(3x) − 1(+4)
5 − 3x − 4
5 − 4 − 3x
1 − 3x
Now I can solve in the usual manner:
1 - 3x = 1
-1 -1
-----------
-3x = 0
--- --
-3 -3
x = 0
Is "x = 0" a valid solution? Yes, indeed, it is, because zero is a valid number. It's not that the solution is "nothing"; it's that the solution is "something", and that this "something" is zero. So my answer is:
x = 0
Affiliate
Advertisement
Students can generally become comfortable with zero being the solution to an equation, but the difference between a solution of "zero" (that solution being a numerical value) and "nothing" (being possibly a physical measure of something like "no apples" or "no money") can cause confusion.
Please make sure that you understand that "zero" itself is not "nothing". Zero is a numerical value which (in "real life" or in the context of a word problem) might imply that there is "nothing" of something or other, but zero itself is a real thing; it exists; it is "something".
-
Solve 11 + 3x − 7 = 6x + 5 − 3x
First, combine like terms; then solve:
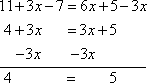
Um... wait just one minute...
Since when is four ever equal to five? Never! Is there any possible x-value that will "fix" this equation, to make it say something that makes any sense? Will any value of x ever make this equation work?
No; it's simply not possible. I did all of my steps correctly, but those steps led to an equation (a) contained no variable and (b) made no sense. Since there is no x-value that will make this equation work, then there is no solution to this equation. And that's my answer for this exercise:
no solution
Here's the logic for the above example: When you try to solve an equation, you are starting from the (unstated) assumption that there actually is a solution. When you end up with nonsense (like the nonsensical equation "4 = 5" above), this means that your initial assumption (namely, that the original equation actually had a solution) was wrong; in fact, there is no solution. Since the statement "4 = 5" is utterly false, and since there is no value of x that ever could make it true, then this equation has no solution.
Advisory: This answer is entirely unlike the answer to the first exercise at the top of this page, where there was a value of x that would work (that solution value being zero). Don't confuse these two very different situations: "the solution exists and has the value of zero" is not in any manner the same as "no solution value exists at all".
Content Continues Below
And don't confuse the "no solution" type of equation above with the following type of equation:
-
Solve 6x + 5 − 2x = 4 + 4x + 1
First, I'll combine like terms; then I'll solve:
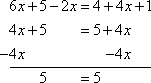
For the previous equation, I ended up with "5 = 4", and there was no value of x that could possibly make the equation true. This result is the opposite of that. For this equation, is there any possible value of x that could make the above statement false? No; 5 is always going to be equal 5. In fact, since there is no "x" in the last line of computations above, the value of x is clearly irrelevant to the equation; x can be anything I want, and the equation will still be true. So the solution is:
all x
This solution could also be stated as "all real numbers", "all reals", "the entire number line", "(−∞, +∞)", or "x ∈ ℝ" (this last meaning "x is a member of the set of real numbers"). You should expect to see some variation in lingo from one textbook or instructor to the next, so don't be surprised at differences in formatting.
Note that, if I had solved the equation by subtracting a 5 from either side of the original equation, I would have ended up with:
4x = 4x
Affiliate
In other words, I would have ended up with another trivially-true statement. I also could have subtracted 4x from either side, or I could have divided both sides of the above equation by 4, or I could have divided through by 4 and then subtracted x from either side, or I could have subtracted both 4x and 5 from both sides of the original equation. Each of these is another way to end up with another trivially-true result, such as "0 = 0". But no matter the specific steps taken, the result (a trivially-true equation) will always be the same, and solution will still be the same: "all x".
Since (as I've listed above) there are many ways of arriving at the same conclusion for this type of equation, you should not be surprised if, for "all real numbers" or "no solution" equations, you didn't use the exact same steps as some of your classmates. There are infinitely-many always-true equations (like "0 = 0") and infinitely-many nonsensical equations (like "3 = 4"), there will also be many ways of (correctly) arriving at these answers.
The main take-away from the above examples should be the following rules:
x = 0: regular solution to regular equation
nonsense (like 3 = 4): no solution
trivially-true (like 0 = 0): solution is all real numbers
Unfortunately, while you'll almost certainly see at least one of these "no solution" or "all reals" questions on the next test (and probably also on the final), there usually aren't many in the homework set, and your instructor probably provided only one example of each type. That doesn't give you much practice at interpreting these types of solutions, so let's so some more examples.
-
Solve 3(x + 4) = 3x + 11
First, I'll multiply the 3 through the parenthetical on the left-hand side. Then I'll solve.
3x + 12 = 3x + 11
-3x -3x
------------------
12 = 11
My math was correct, but the result is nonsense. Twelve is never going to equal eleven. So my answer is:
no solution
-
Solve 6 − 2(x + 3) = −2x
I'll multiply through and simplify on the left-hand side. Then I'll solve.
6 - 2(x + 3) = -2x
6 - 2x - 6 = -2x
6 - 6 - 2x = -2x
0 - 2x = -2x
-2x = -2x
+2x +2x
---------
0 = 0
Zero is always going to be equal to zero, and there's not even any variable in the last line of my work, so the variable is clearly irrelevant. This equation is true, regardless of the value of x. So my answer is:
all x
-
Solve 2(x + 1) + x = 3(x + 2) − 2
I'll need to multiply through and simplify on each side of this equation.
2(x + 1) + x = 3(x + 2) - 2
2x + 2 + x = 3x + 6 - 2
2x + x + 2 = 3x + 4
3x + 2 = 3x + 4
-3x -3x
----------------------
2 = 4
Nope; never true.
no solution
-
Solve 5x + 7 = 4(2x + 1) − 3x − 2
I need to simplify the right-hand side, and then see where that leads.
5x + 7 = 4(2x + 1) - 3x - 2
5x + 7 = 8x + 4 - 3x - 2
5x + 7 = 8x - 3x + 4 - 2
5x + 7 = 5x + 2
-5x -5x
------------------
7 = 2
Nope; never true.
no solution
Affiliate
-
Solve 8(x + 2) = 2x + 16
I'll expand the left-hand side, and then solve.
8(x + 2) = 2x + 16
8x + 16 = 2x + 16
-2x -2x
------------------
6x + 16 = 16
-16 -16
------------------
6x + 0 = 0
------ -
6 6
x = 0
This equation does have a solution value, being the value of zero.
x = 0
-
Solve 1.5x + 4 = 4(x + 1) − 2.5x
I'll expand and simplify on the right-hand side, and then solve.
1.5x + 4 = 4(x + 1) - 2.5x
1.5x + 4 = 4x + 4 - 2.5x
1.5x + 4 = 4x - 2.5x + 4
1.5x + 4 = 1.5x + 4
-1.5x -1.5x
--------------------
4 = 4
This is always true, so my answer is:
(−∞, +∞)
-
Solve 2(x + 5) = 2x + 5
I'll expand the left-hand side, and then solve.
2(x + 5) = 2x + 5
2x + 10 = 2x + 5
-2x -2x
-----------------
10 = 5
Nope; never true.
no solution
URL: https://www.purplemath.com/modules/solvelin5.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()



