The Factor Theorem
Purplemath
The Factor Theorem is a result of the Remainder Theorem, and is based on the same reasoning. If you haven't read the lesson on the Remainder Theorem, review that topic first, and then return here.
Content Continues Below
As the Remainder Theorem points out, if you divide a polynomial p(x) by a factor x − a of that polynomial, then you will get a zero remainder.
This is similar to what you learned back in grammar school; namely, if you divide a number by a factor of that number, then you'll get a zero remainder. For example, if you take 15 and divide it by 3, you'll get a zero remainder; the 3 divided into the 15 "evenly" because 3 is a factor of 15. On the other hand, if you divided 15 by 4, you'd get a remainder of 3, because 4 is not a factor of 15.
This is easy enough to understand when we're dealing with simple whole numbers. It can get a bit confusing when we're dealing with polynomial expressions. So let's look again at the Division Algorithm expression for polynomials:
What is the Division Algorithm for Polynomials?
The Division Algorithm for Polynomials: Given a polynomial p(x) and a linear divisor (x − a), the polynomial can be restated as:
p(x) = (x − a)q(x) + r(x)
...where q(x) is the quotient and r(x) is the remainder.
If x − a is indeed a factor of p(x), then the remainder after division by x − a will be zero. That is, r(x) = 0, and you get:
p(x) = (x − a)q(x)
In terms of the Remainder Theorem, this means that, if x − a is a factor of p(x), then the remainder r(x), when we do synthetic division by x = a, will be zero.
Affiliate
Advertisement
What does the Factor Theorem say?
The point of the Factor Theorem is the reverse of the Remainder Theorem: If you synthetic-divide a polynomial by x = a and get a zero remainder, then not only is x = a a zero of the polynomial (courtesy of the Remainder Theorem), but also x − a is a factor of the polynomial. (Why? It's courtesy of the Factor Theorem.)
How do you use the Factor Theorem (in math)?
Just as with the Remainder Theorem, the point of the Factor Theorem is not to do the long division of a given polynomial by a given factor. When faced with a Factor Theorem exercise, you will instead apply synthetic division and then check for a zero remainder. This Theorem isn't repeating what you already know, but is instead trying to make your life simpler.
- Use the Factor Theorem to determine whether x − 1 is a factor of f(x) = 2x4 + 3x2 − 5x + 7.
For x − 1 to be a factor of f(x) = 2x4 + 3x2 − 5x + 7, the Factor Theorem says that x = 1 must be a zero of f(x).
To test whether x − 1 is a factor, I will first set x − 1 equal to zero and solve to find the proposed zero:
x − 1 = 0
x = 1
So I need to plug 1 into my synthetic division. Since there is no cubed term in the polynomial they've given me, I will be careful to remember to insert a "0" into the first line of the synthetic division to represent the omitted power of x in 2x4 + 3x2 − 5x + 7. So I plug-n-chug:
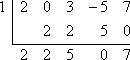
Since the remainder is not zero, then the Factor Theorem tells me that:
x − 1 is not a factor of f(x).
Content Continues Below
What is an example of factoring with the Factor Theorem?
- Using the Factor Theorem, verify that x + 4 is a factor of f(x) = 5x4 + 16x3 − 15x2 + 8x + 16.
If x + 4 is a factor, then (setting this factor equal to zero and solving) x = −4 is a root. To do the required verification, I need to check that, when I use synthetic division on f (x), with x = −4, I get a zero remainder:
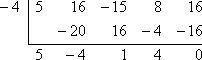
The remainder is zero, so the Factor Theorem says that:
x + 4 is a factor of 5x4 + 16x3 − 15x2 + 8x + 16.
Affiliate
In practice, the Factor Theorem is used when factoring polynomials "completely". Rather than trying various factors by using long division, you will use synthetic division and the Factor Theorem. Any time you divide by a number (that number being a potential root of the polynomial) and get a zero remainder in the synthetic division, this means that the number is indeed a root, and thus "x minus the number" is a factor. Then you will continue the division with the resulting smaller polynomial, repeating the process until you arrive at a linear factor (at which point, you've found all the factors) or a quadratic (to which you can apply the Quadratic Formula).
- Using the fact that −2 and are zeroes of f(x) = 3x4 + 5x3 + x2 + 5x − 2, factor the polynomial completely.
Since x = −2 is a zero of the given polynomial, then I know that x + 2 = 0, so x + 2 is a factor.
Similarly, since is a zero, then , so is a factor.
In other words, by giving me two of the zeroes, they have also given me two of the factors; namely, x + 2 and .
Since I started with a fourth-degree polynomial, then I'll be left with a quadratic once I divide out these two given factors. I can solve that final quadratic by using the Quadratic Formula or some other method.
The Factor Theorem says that I don't have to do the long division with the known factors of x + 2 and . Instead, I can use synthetic division with the associated zeroes −2 and . Here is what I get when I do the first division with x = −2:
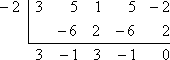
The remainder is zero, which is expected because they'd told me at the start that −2 was a known zero of the polynomial.
Rather than starting over again with the original polynomial, I'll now work on the remaining polynomial of 3x3 − x2 + 3x − 1 (from the bottom line of the previous synthetic division). I will divide this by the other given zero, :
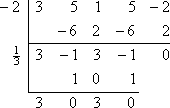
This leaves me with the quadratic 3x2 + 3, which I can solve:
3x2 + 3 = 0
3(x2 + 1) = 0
x2 + 1 = 0
x2 = −1
x = ± i
Since the zeroes of the remaining quadratic factor are x = −i and x = i, then the factors are x − (−i) and x − (i), or x + i and x − i.
When I write out my factorization, I need to remember that I divided off a "3" when I solved the quadratic; it is still part of the polynomial, and needs to be included as a factor. Then the fully-factored form is:
(If you haven't yet studied complex numbers, then you'd stop at .)
URL: https://www.purplemath.com/modules/factrthm.htm
You can use the Mathway widget below to practice finding a polynomial's factors using the Factor Theorem. Try the entered exercise, or type in your own exercise. Then click the button and select "Find the Factors Using the Factor Theorem" to compare your answer to Mathway's.
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()




