The Remainder Theorem
Purplemath
The Remainder Theorem is useful for evaluating polynomials at a given value of x, though it might not seem so, at least at first blush. This is because the tool is presented as a theorem with a proof, and you probably don't feel ready for proofs at this stage in your studies.
Fortunately, you don't "have" to understand the proof of the Theorem; you just need to understand how to use the Theorem.
Content Continues Below
The Remainder Theorem starts with an unnamed polynomial p(x), where "p(x)" just means "some polynomial p whose variable is x". Then the Theorem talks about dividing that polynomial by some linear factor x − a, where a is just some number.
Then, as a result of the long polynomial division, you end up with some polynomial answer q(x), with the "q" standing for "the quotient polynomial"; and some remainder r(x), the r standing for "the remainder, after division". This remainder may be a proper variable-containing polynonial, or it may be just a number.
As a concrete example of p, a, q, and r, let's look at the polynomial p(x) = x3 − 7x − 6, and let's divide by the linear factor x − 4 (so a = 4):
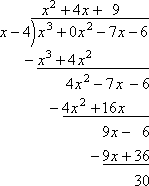
So we get a quotient of q(x) = x2 + 4x + 9 on top, with a remainder of r(x) = 30.
Affiliate
Advertisement
Back when you were learning about long division of regular numbers, you learned that your remainder (if there was one) had to be smaller than whatever you had divided by. In polynomial terms, since we're dividing by a linear factor (that is, a factor in which the degree on x is just an understood "1"), then the remainder must be a constant value. That is, when you divide any polynomial by the linear divisor "x − a", your remainder will, and must, be just some plain number.
The Remainder Theorem thus points out the connection between division and multiplication. For instance, since 12 ÷ 3 = 4, then 4 × 3 = 12. If your division ends with a non-zero remainder left over, then, when you go the other way and do the multiplication, you'll need to add that remainder back in. For example, since:
13 ÷ 5 = 2 R 3
...then, going back the other way with multiplication, you'll get:
13 = 5 × 2 + 3
This process works the same way with polynomials. That is:
If:
p(x) ÷ (x − a) = q(x)
with remainder r(x)
...then:
p(x) = (x − a) q(x) + r(x)
(Technically, this "if - then" statement is the "Division Algorithm for Polynomials". But the Algorithm is the basis for the Remainder Theorem.)
In terms of our concrete example from above:
Since:
(x^3 − 7x − 6) ÷ (x − 4) = x2 + 4x + 9
with remainder 30
...then:
x3 − 7x − 6 = (x − 4) (x2 + 4x + 9) + 30
Content Continues Below
Why all this tiresome review of division? Because, for polynomials, dividing by a linear factor x − a and finding the numerical remainder tells us the value of the polynomial when evaluated at x = a; in other words, the Theorem gives us a shorthand way to evaluate polynomials.
The Division Algorithm for polynomials says that we can restate a polynomial in terms of its divisor x − a, its quotient, and its remainder. Once reformatted this way, we can then evaluate the polynomial at x = a. But when x = a, then the divisor x − a is a − a, which is zero! So evaluating the polynomial at x = a gives us the following result:
p(a) = (a − a)q(a) + r(a)
= (0)q(a) + r(a)
= 0 + r(a)
= r(a)
And remember that the remainder term r(a) is just a number! So the value of the polynomial p(x) at x = a is the same as the remainder you get when you divide that polynomial p(x) by x − a.
What does the Remainder Theorem say?
The Remainder Theorem tells us that, in order to evaluate a polynomial p(x) at some number x = a, we can instead divide by the linear expression x − a. The remainder, r(a), gives the value of the polyomial at x = a.
In terms of our concrete example:
p(4) = (4 − 4)((4)2 + 4(4) + 9) + 30
= (0)(16 + 16 + 9) + 30
= 0 + 30
= 30
Affiliate
But you gotta think: Okay, fine; the value of the polynomial p(x) at x = a is the remainder r(a) when you divide by x − a, but who wants to do the long division each time you have to evaluate a polynomial at a given value of x?!? You're right; doing the long division every time would indeed be overkill. Fortunately, that's not what they really want you to do.
When you are dividing by a linear factor, you don't have to use long polynomial division; instead, you can use synthetic division, which is much quicker. In our concrete example, we would get:

Note that the last entry in the bottom row is 30, the remainder from the long division (as expected) and also the value of p(x) = x3 − 7x − 6 at x = 4. And that is the point of the Remainder Theorem:
What is the point of the Remainder Theorem?
The point of the Remainder Theorem is that there is a simpler, quicker way to evaluate a polynomial p(x) at a given value of x, and this simpler way is to not evaluate p(x) at all, but to instead do the synthetic division at that same value of x. The last number in the synthetic-division result is the value you're wanting, being the evaluated value of the polyomial.
What is an example of using the Remainder Theorem?
- Use the Remainder Theorem to evaluate f(x) = 6x3 − 5x2 + 4x − 17 at x = 3.
First off, even though the Remainder Theorem refers to the polynomial and to long division and to restating the polynomial in terms of a quotient, a divisor, and a remainder, blah, blah, blah, that's not actually what I'm meant to be doing. Instead, I'm supposed to be doing synthetic division, using "3" as the divisor:
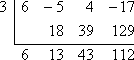
Since the remainder (the last entry in the bottom row) is 112, then the Remainder Theorem says that:
f (3) = 112.
- Using the Remainder Theorem, find the value of f (−5), for f (x) = 3x4 + 2x3 + 4x.
I need to do the synthetic division, remembering to put zeroes in for the powers of x that are not included in the polynomial:
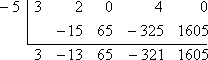
Since the remainder is 1605, then, thanks to the Remainder Theorem, I know that:
f (−5) = 1605.
What if the remainder, after division, is zero? What does this mean?
Well, first, it means that the polynomial evaluates to zero at whatever x-value you used in your synthetic division. But, second, it says that there is no (interesting) remainder; a remainder of zero means that you divided by x − a and had nothing left over, so x − a must be a factor of the polynomial.
- Use the Remainder Theorem to determine whether x = 2 is a zero of f (x) = 3x7 − x4 + 2x3 − 5x2 − 4
For x = 2 to be a zero of f (x), then f (2) must evaluate to zero. In the context of the Remainder Theorem, this means that my remainder, when dividing by x = 2, must be zero. Here's my division:
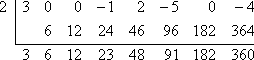
I see that the remainder is not zero; it is in fact 360. This tells me that:
x = 2 is not a zero of f (x)
- Use the Remainder Theorem to determine whether x = −4 is a solution of x6 + 5x5 + 5x4 + 5x3 + 2x2 − 10x − 8 = 0
For x = −4 to be a solution of f (x) = x6 + 5x5 + 5x4 + 5x3 + 2x2 − 10x − 8 = 0, it must be that f (−4) = 0. In the context of the Remainder Theorem, this means that the remainder, when dividing by x = −4, must be zero:

The remainder is actually zero. This tells me that:
x = −4 is a solution.
URL: https://www.purplemath.com/modules/remaindr.htm
You can use the Mathway widget below to practice evaluating a polynomial using the Remainder Theorem. Try the entered exercise, or type in your own exercise. Then click the button and select "Evaluate Using the Remainder Theorem" to compare your answer to Mathway's.
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()




