Synthetic Division: The Process
Purplemath
What is synthetic division?
Synthetic division is a shorthand, or shortcut, method of polynomial division in the special case of dividing by a linear factor — and it only works in this case. Synthetic division is generally used, however, not for dividing out factors but for finding zeroes (or roots) of polynomials. More about this later.
Content Continues Below
How are polynomial zeroes and factors related?
If you are given, say, the polynomial equation y = x2 + 5x + 6, you can factor the polynomial as y = (x + 3)(x + 2). Then you can find the zeroes of y by setting each factor equal to zero and solving. You will find that the two zeroes of the polynomial are x = −2 and x = −3.
Affiliate
Advertisement
You can, however, also work backwards from the zeroes to find the originating polynomial. For instance, if you are given that x = −2 and x = −3 are the zeroes of a quadratic, then you know that x + 2 = 0, so x + 2 is a factor, and x + 3 = 0, so x + 3 is a factor. Therefore, you know that the quadratic must be of the form y = a(x + 3)(x + 2).
(The extra number "a" in that last sentence is in there because, when you are working backwards from the zeroes, you don't know toward which quadratic you're working. For any non-zero value of "a", your quadratic will still have the same zeroes. But the issue of the value of "a" is just a technical consideration; as long as you see the relationship between the zeroes and the factors, that's all you really need to know for this lesson.)
Anyway, the above is a long-winded way of saying that, if x − n is a factor, then x = n is a zero, and if x = n is a zero, then x − n is a factor. And this is the fact you use when you do synthetic division.
Affiliate
Let's look again at the quadratic from above: y = x2 + 5x + 6. From the Rational Roots Test, we know that ± 1, 2, 3, and 6 are possible zeroes of the quadratic. (And, from the factoring above, we know that the zeroes are, in fact, −3 and −2.) How would you use synthetic division to check the potential zeroes?
Well, think about how long polynomial divison works. If I were to guess that x = 1 is a zero, then this means that x − 1 is a factor of the quadratic. And if it's a factor, then it will divide out evenly; that is, if we divide x2 + 5x + 6 by x − 1, we would get a zero remainder. Let's check:
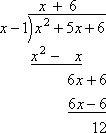
As expected (since we know that x − 1 is not a factor), we got a non-zero remainder. What does this look like in synthetic division?
Content Continues Below
How do you do synthetic division?
First, take the polynomial (in our case, x2 + 5x + 6), and write the coefficients ONLY inside an upside-down division-type symbol:
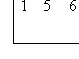
Make sure you leave room inside, underneath the row of coefficients, to write another row of numbers later.
Put the test zero, in our case x = 1, at the left, next to the (top) row of numbers:
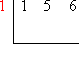
Take the first number that's on the inside, the number that represents the polynomial's leading coefficient, and carry it down, unchanged, to below the division symbol:
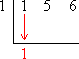
Multiply this carry-down value by the test zero on the left, and carry the result up into the next column inside:
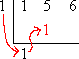
Add down the column:
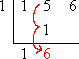
Multiply the previous carry-down value by the test zero, and carry the new result up into the last column:
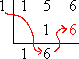
Add down the column:
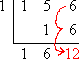
This last carry-down value is the remainder.
Comparing, you can see that we got the same result from the synthetic division, the same quotient (namely, 1x + 6) and the same remainder at the end (namely, 12), as when we did the long division:
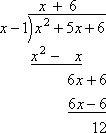
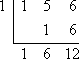
The results are formatted differently, but you should recognize that each format provided us with the same result, being a quotient of x + 6, and a remainder of 12.
We already know (from the factoring above) that x + 3 is a factor of the polynomial, and therefore that x = −3 is a zero.
Now let's compare the results of long division and synthetic division when we use the factor x + 3 (for the long division) and the zero x = −3 (for the synthetic division):
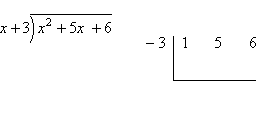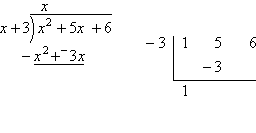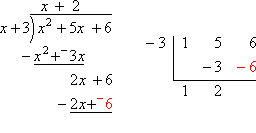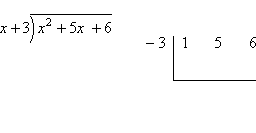
As you can see above, while the results are formatted differently, the results are otherwise the same:
In the long division, I divided by the factor x + 3, and arrived at the result of x + 2 with a remainder of zero. This means that x + 3 is a factor, and that x + 2 is left after factoring out the x + 3. Setting the factors equal to zero, I get that x = −3 and x = −2 are the zeroes of the quadratic.
In the synthetic division, I divided by x = −3, and arrived at the same result of x + 2 with a remainder of zero. Because the remainder is zero, this means that x + 3 is a factor and x = −3 is a zero. Also, because of the zero remainder, x + 2 is the remaining factor after division. Setting this equal to zero, I get that x = −2 is the other zero of the quadratic.
I will return to this relationship between factors and zeroes throughout what follows; the two topics are inextricably intertwined.
URL: https://www.purplemath.com/modules/synthdiv.htm
You can use the Mathway widget below to practice doing synthetic division. Try the entered exercise, or type in your own exercise. Then click the button to compare your answer to Mathway's. (Or skip the widget and continue to the next page.)
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()




