Polynomial Division: Simplification
Purplemath
There are two cases for dividing polynomials: either the "division" is really just a simplification and you're just reducing a fraction (albeit a fraction containing polynomials), or else you need to do long polynomial division (which is explained on the next page). We'll start with reduction of a fraction.
-
Simplify
This "division" is just a simplification problem, because there is only one term in the polynomial that they're having me dividing by. And, in this case, there is a common factor in the numerator (top) and denominator (bottom), so it's easy to reduce this fraction.
Content Continues Below
There are two ways of proceeding. I can split the division into two fractions, each with only one term on top, and then reduce each of the two fractions separately:
...or else I can factor out the common factor from the top and bottom, and then cancel off this common factor:
Either way, my answer is the same:
x + 2
Note: Some students try to "cancel" before factorization. This cannot work! Fractions have "understood" parentheses around their numerators or denominators.
It is necessary to include these explicitly when typing fractions out sideways, such as "(2x + 4)/2", so it's clear what, exactly, is on top and what is underneath. Otherwise, the typed version would likely be mis-understood to mean "2x + 4/2 = 2x + 2", which is not what was intended.
Students may try to do this:
This is wrong! Don't do this!
Even when the fractions are typeset in the math-book upright way, don't forget that there are (invisible) parentheses around the numerator and denominator, especially if the top or the bottom of the fraction has more than one term.
When simplifying polynomial fractions, you can never reach inside those "understood" parentheses around the numerator and denominator, ripping arms and legs off of the polynomials within! (The poor little polynomials' big brown eyes are welling up with tears, just thinking about it!)
Instead, you must factor, and then only cancel off common factors, if any. In other words, for the exercise above, you must do the following:
![(2x + 4)/2 is factored: [2(x + 2)]/[2(1)]; then the 2's are cancelled off: (x + 2)/1 = x + 2](polys/div02B.gif)
This is the way to go.
-
Simplify
Again, I can solve this in either of two ways. One way is to simplify by splitting up the sum and then simplifying each fraction separately:
![21x^3/7x − 35x^2/7x = [7x(3x^2)]/[7x] − [7x(5x)]/[7x] = 3x^2 − 5x](polys/div03.gif)
The other way is to simplify by taking the common factor of the numerator and denominator out front and then canceling it off:
![[7x(3x^2 − 5x)]/[7x] = 3x^2 − 5x](polys/div04.gif)
Either way, my answer is the same:
3x2 − 5x
Content Continues Below
Note: Most books don't talk about the domain at this point. But if your book does, you will need to note, for the above simplification, that x cannot equal zero.
Why? Because, in the original (unsimplified) form, letting x equal 0 would have caused division by zero. That's not allowed. So the original form could not allow x to equal zero. However, in the simplified form, there is no way to know about this original-form restriction. For the simplified form to be mathematically equal to the original expression, the simplified form would need to be "3x2 − 5x, for all x ≠ 0".
But this is a technical point and, if your book doesn't mention anything about this now, then don't worry about it for the time being.
-
Simplify
I can split the difference in the numerator to get the difference of two fractions, and then I can reduce each fraction separately. Each will have a factor of x + 3 in the numerator which will cancel with the denominator.
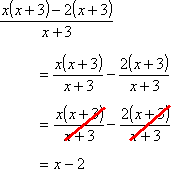
Or, alternatively, I can note that the terms in the numerator do indeed have a common factor; it's just that this common factor is rather large. Since both terms in the numerator contain the factor "x + 3", then this is a common factor, and it can be factored out front. Then the big factor out front will cancel with the denominator:
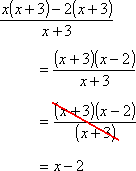
Either way, my simplified answer is the same:
x − 2
You can use the Mathway widget below to practice doing simple polynomial division. Try the entered exercise, or type in your own exercise. Then click the button to compare your answer to Mathway's.
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
URL: https://www.purplemath.com/modules/polydiv.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()



