Synthetic Division: Examples
Purplemath
Once you've been introduced to synthetic division, you'll want to practice in order to become familiar with the synthetic-divison process. What follows are two worked examples.
The first example is just synthetic division, where you're given the synthetic-division set-up and all you have to do is apply the process.
Content Continues Below
The second is an example of an exercise in which you are expected to figure out the synthetic-division set-up, given a polynomial and a linear divisor; do the division, and then extract the answer, in the form of a polynomial and a rational-expression remainder.
- Complete the indicated division.

For this first exercise, I will display the entire synthetic-division process step-by-step.
First, carry down the "2" that indicates the leading coefficient:

Multiply by the number on the left, and carry the result into the next column:

Add down the column:
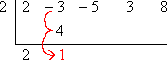
Multiply by the number on the left, and carry the result into the next column:

Add down the column:
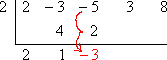
Multiply by the number on the left, and carry the result into the next column:

Add down the column:

Multiply by the number on the left, and carry the result into the next column:

Add down the column for the remainder:

The completed division is:

This exercise never said anything about polynomials, factors, or zeroes. But this division tells us that, if we divide the polynomial 2x4 − 3x3 − 5x2 + 3x + 8 by the linear divisor x − 2, then the remainder will be 2, and therefore x − 2 is not a factor of 2x4 − 3x3 − 5x2 + 3x + 8, and x = 2 is not a zero (that is, a root or x-intercept) of the initial polynomial.
Note: The divisor in synthetic division is not only linear, but it also has a leading coefficient of 1.
Content Continues Below
- Divide 3x3 − 2x2 + 3x − 4 by x − 3 using synthetic division. Write the answer in the form "".
This question is asking me, in effect, to convert an "improper" polynomial "fraction" into a polynomial "mixed number". That is, I am being asked to do something similar to converting the improper fraction to the mixed number , which is really the shorthand for the addition expression .
In order for me to convert the polynomial division into the required "mixed number" format, I have to do the synthetic division. I will show most of the steps.
First, I write down all the coefficients, and put the zero from x − 3 = 0 (so x = 3) at the left.
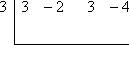
Next, I carry down the leading coefficient from the polynomial dividend (that is, the polynomial's coefficients inside the synthetic-division set-up):
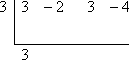
Advertisement
Now I multiply by the potential zero, carry the result up to the next column, and add down:
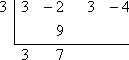
I repeat this process:
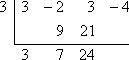
Lather, rinse, repeat:
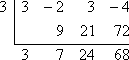
As you can see, the remainder is 68.
Since I started with a polynomial of degree 3 and then divided by x − 3 (that is, since I divided by a polynomial of degree 1), I am left with a polynomial of degree 2. Then the bottom line represents the polynomial3x2 + 7x + 24 with a remainder of 68. Putting this result into the required "mixed number" format, I get the answer as being:
It is always true that, when you use synthetic division, your answer (in the bottom row) will be a polynomial of degree less, by one, than what you'd started with, because you have divided out a linear factor. I had started with a cubic, so I knew that my answer, denoted by the "3 7 24" in the bottom row, stood for a quadratic.
URL: https://www.purplemath.com/modules/synthdiv2.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()




