Zeroes and Their Multiplicities
Purplemath
The real (that is, the non-complex) zeroes of a polynomial correspond to the x-intercepts of the graph of that polynomial. So we can find information about the number of real zeroes of a polynomial by looking at the graph and, conversely, we can tell how many times the graph is going to touch or cross the x-axis by looking at the zeroes of the polynomial (or at the factored form of the polynomial).
A zero has a "multiplicity", which refers to the number of times that its associated factor appears in the polynomial. For instance, the quadratic (x + 3)(x − 2) has the zeroes x = −3 and x = 2, each occuring once. The eleventh-degree polynomial (x + 3)4(x − 2)7 has the same zeroes as did the quadratic, but in this case, the x = −3 solution has multiplicity 4 because the factor (x + 3) occurs four times (that is, the factor is raised to the fourth power) and the x = 2 solution has multiplicity 7 because the factor (x − 2) occurs seven times.
Content Continues Below
-
List the zeroes, with their multiplicities, of the polynomial function y = 3(x + 5)3 (x + 2)4 (x − 1)2 (x − 5)
The zeroes of the function (and, yes, "zeroes" is the correct way to spell the plural of "zero") are the solutions of the linear factors they've given me. Solving each factor gives me:
x + 5 = 0 ⇒ x = −5
x + 2 = 0 ⇒ x = −2
x − 1 = 0 ⇒ x = 1
x − 5 = 0 ⇒ x = 5
The multiplicity of each zero is the number of times that its corresponding factor appears. In other words, the multiplicities are the powers. (For the factor x − 5, the understood power is 1.) Then my answer is:
x = −5 with multiplicity 3
x = −2 with multiplicity 4
x = 1 with multiplicity 2
x = 5 with multiplicity 1
Affiliate
Affiliate
The point of multiplicities with respect to graphing is that any factors that occur an even number of times (that is, any zeroes that occur twice, four times, six times, etc) are squares, so they don't change sign. Squares are always positive. This means that the x-intercept corresponding to an even-multiplicity zero can't cross the x-axis, because the zero can't cause the graph to change sign from positive (above the x-axis) to negative (below the x-axis), or vice versa.
The practical upshot is that an even-multiplicity zero makes the graph just barely touch the x-axis, and then turns it back around the way it came. You can see this in the following graphs:
y = (x + 6)(x − 7)
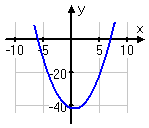
x = −6 once
x = 7 once
y = (x + 6)(x − 7)2
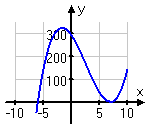
x = −6 once
x = 7 twice
y = (x + 6)2 (x − 7)
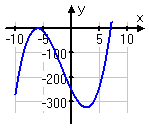
x = −6 twice
x = 7 once
y = (x + 6)2(x − 7)2
x = −6 twice
x = 7 twice
All four graphs have the same zeroes, at x = −6 and at x = 7, but the multiplicity of the zero determines whether the graph crosses the x-axis at that zero or if it instead turns back the way it came. If the zero was of multiplicity 1, the graph crossed the x-axis at the zero; if the zero was of multiplicity 2, the graph just "kissed" the x-axis before heading back the way it came.
Any zero whose corresponding factor occurs in pairs (so two times, or four times, or six times, etc) will "bounce off" the x-axis and return the way it came. Any zero whose corresponding factor occurs an odd number of times (so once, or three times, or five times, etc) will cross the x-axis. Polynomial zeroes with even and odd multiplicities will always behave in this way.
Content Continues Below
-
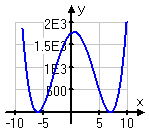
The following graph shows an eighth-degree polynomial. List the polynomial's zeroes with their multiplicities.

I can see from the graph that there are zeroes at x = −15, x = −10, x = −5, x = 0, x = 10, and x = 15, because the graph touches or crosses the x-axis at these points. (At least, I'm assuming that the graph crosses at exactly these points, since the exercise doesn't tell me the exact values. When I'm guessing from a picture, I do have to make certain assumptions.)
Advertisement
Since the graph just touches at x = −10 and x = 10, then it must be that these zeroes occur an even number of times. The other zeroes must occur an odd number of times. The odd-multiplicity zeroes might occur only once, or might occur three, five, or more times each; there is no way to tell from the graph. (At least, there's no way to tell yet — we'll learn more about that on the next page.) And the even-multiplicity zeroes might occur four, six, or more times each; I can't tell by looking.
But if I add up the minimum multiplicity of each, I should end up with the degree, because otherwise this problem is asking for more information than is available for me to give. I've got the four odd-multiplicity zeroes (at x = −15, x = −5, x = 0, and x = 15) and the two even-multiplicity zeroes (at x = −10 and x = 10). Adding up their minimum multiplicities, I get:
1 + 2 + 1 + 1 + 2 + 1 = 8
...which is the degree of the polynomial. So the minimum multiplicities are the correct multiplicities, and my answer is:
x = −15 with multiplicity 1,
x = −10 with multiplicity 2,
x = −5 with multiplicity 1,
x = 0 with multiplicity 1,
x = 10 with multiplicity 2, and
x = 15 with multiplicity 1
Affiliate
I was able to compute the multiplicities of the zeroes in part from the fact that the multiplicities will add up to the degree of the polynomial, or two less, or four less, etc, depending on how many complex zeroes there might be. But multiplicity problems don't usually get into complex-valued roots. So, if you're asked to guess multiplicities from a graph, as above, you're probably safe in assuming that all of the roots are real numbers.
URL: https://www.purplemath.com/modules/polyends2.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()



