Polynomial Graphs: End Behavior
Purplemath
When you're graphing (or looking at a graph of) polynomials, it can help to already have an idea of what basic polynomial shapes look like. One of the aspects of this is "end behavior", and it's pretty easy. We'll look at some graphs, to find similarities and differences.
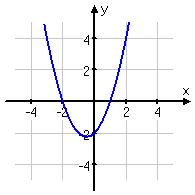
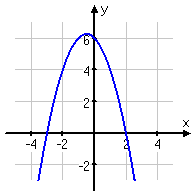
First, let's look at some polynomials of even degree (specifically, quadratics in the first row of pictures, and quartics in the second row) with positive and negative leading coefficients:
Content Continues Below
← swipe to view full table →
with a positive |
with a negative |
|
 |
 |
|
 |
 |
In all four of the graphs above, the ends of the graphed lines entered and left the same side of the picture. When the graphs were of functions with positive leading coefficients, the ends came in and left out the top of the picture, just like every positive quadratic you've ever graphed. When the graphs were of functions with negative leading coefficients, the ends came in and left out the bottom of the picture, just like every negative quadratic you've ever graphed.
These traits will be true for every even-degree polynomial. If you can remember the behavior for quadratics (that is, for parabolas), then you'll know the end-behavior for every even-degree polynomial.
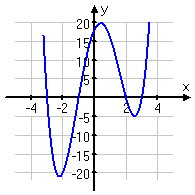
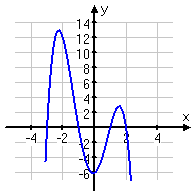
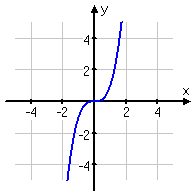
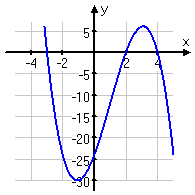
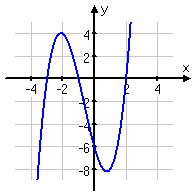
Now let's look at some polynomials of odd degree (cubics in the first row of pictures, and quintics in the second row):
← swipe to view full table →
with a positive |
with a negative |
|
 |
 |
|
 |
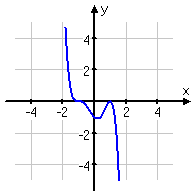 |
As you can see above, odd-degree polynomials have ends that head off in opposite directions. If they start "down" (entering the graphing "box" through the "bottom") and go "up" (leaving the graphing "box" through the "top"), they're positive polynomials, just like every positive cubic you've ever graphed. But If they start "up" and go "down", they're negative polynomials.
This behavior is true for all odd-degree polynomials. If you can remember the behavior for cubics (or, technically, for straight lines with positive or negative slopes), then you will know what the ends of any odd-degree polynomial will do.
All even-degree polynomials behave, on their ends, like quadratics; all odd-degree polynomials behave, on their ends, like cubics.
Content Continues Below
-
Which of the following could be the graph of a polynomial whose leading term is "−3x4"?
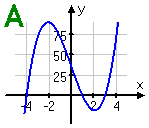
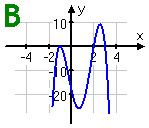
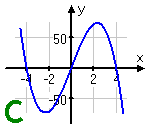
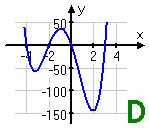
To answer this question, the important things for me to consider are the sign and the degree of the leading term.
The exponent says that this is a degree-4 polynomial; 4 is even, so the graph will behave roughly like a quadratic; namely, its graph will either be up on both ends or else be down on both ends. Since the sign on the leading coefficient is negative, the graph will be down on both ends.
(The actual value of the negative coefficient, −3 in this case, is actually irrelevant for this problem. All I need is the "minus" part of the leading coefficient.)
Clearly Graphs A and C represent odd-degree polynomials, since their two ends head off in opposite directions. Graph D shows both ends passing through the top of the graphing box, just like a positive quadratic would. The only graph with both ends down is:
Graph B
Affiliate
-
Describe the end behavior of f (x) = 3x7 + 5x + 1004
This polynomial is much too large for me to view in the standard screen on my graphing calculator, so either I can waste a lot of time fiddling with WINDOW options, or I can quickly use my knowledge of end behavior.
This function is an odd-degree polynomial, so the ends go off in opposite directions, just like every cubic I've ever graphed. A positive cubic enters the graph at the bottom, down on the left, and exits the graph at the top, up on the right. Since the leading coefficient of this odd-degree polynomial is positive, then its end-behavior is going to mimic that of a positive cubic. Therefore, the end-behavior for this polynomial will be:
"Down" on the left and "up" on the right.
URL: https://www.purplemath.com/modules/polyends.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()



