x- and y-Intercepts
Purplemath
What are intercepts?
Intercepts are places where a graph crosses, or at least touches, an axis. While dictionaries define "intercept" as a verb that refers to stopping or blocking something from continuing on its way, an intercept in mathematics is a noun that refers to a crossing point.
Content Continues Below
What are x-intercepts and y-intercepts?
An x-intercept is where a graph crosses (or at least touches) the x-axis (that is, the horizontal axis); a y-intercept is where the graph crosses (or just touches) the y-axis (that is, the vertical axis).
So the graphical concept of x- and y-intercepts is pretty simple. The problems start when we are required to try to deal with intercepts algebraically.
To clarify the algebraic part, think again about the axes. When you were first introduced to the Cartesian plane, you were shown the regular number line from elementary school (that is, the x-axis), and then shown how you could draw a perpendicular number line (that is, the y-axis) through the zero point on the first number line.
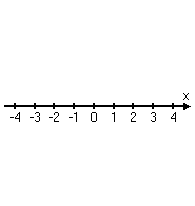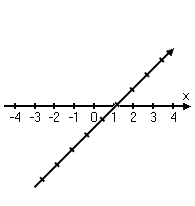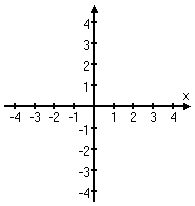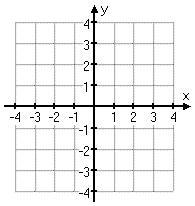
(The above image is animated on the live web page.)
Affiliate
The y-axis corresponds to the vertical line x = 0; the x-axis corresponds to the horizontal line y = 0
Advertisement
This means that, algebraically,
- an x-intercept is a point on the graph where y is zero, and
- a y-intercept is a point on the graph where x is zero.
More specifically,
- an x-intercept is a solution to the equation when the y-value has been set to zero, and
- a y-intercept is a solution to the equation when the x-value has been set to zero.
This understanding of intercepts as solutions to equations allows us to establish the algebraic process for finding intercepts.
How do you find x-intercepts and y-intercepts?
To find one axis' intercept(s), set the other variable equal to zero, and solve the resulting equation. If there are no solutions to that equation, then there are no intercepts on that axis.
- To find the y-intercept(s), set x equal to zero, and solve the equation; the y-values of the solutions, if any, say where the graph of the equation crosses or touches the y-axis.
- To find the x-intercept(s), set y equal to zero, and solve the equation; the x-values of the solutions, if any, say where the graph of the equation crosses or touches the x-axis.
Historical oddity: While the y-intercept was defined in 1881, the x-intercept wasn't defined until 1905. I have no idea why there was that twenty-four year gap.
Content Continues Below
- Find the x- and y-intercepts of x2 + 4y2 = 9.
Using the definitions of the intercepts, I will proceed as follows:
x-intercept(s):
y = 0 for the x-intercept(s), so:
25x2 + 4y2 = 9
25x2 + 4(0)2 = 9
25x2 + 0 = 9
Then the x-intercepts are the following two points:
y-intercept(s):
x = 0 for the y-intercept(s), so:
25x2 + 4y2 = 9
25(0)2 + 4y2 = 9
0 + 4y2 = 9
Then the y-intercepts are the following two points:
Just remember: Whichever intercept you're looking for, the other variable gets set to zero.
Affiliate
In addition to the above considerations, you should think of the following terms interchangeably:
- x-intercept
- roots
- solutions
- zeroes
In other words, the following exercises are equivalent:
- Find the x-intercept(s) of y = x3 + 2x2 − x − 3
- Solve x3 + 2x2 − x − 3 = 0
- Find the zeroes / roots of f (x) = x3 + 2x2 − x − 3
If you keep this equivalence in the back of your head, many exercises will make a lot more sense. For instance, if they give you something like the following graph:
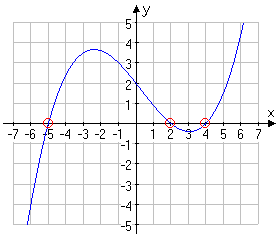
...and then they ask you to find the "solutions", you'll know that they mean "find the x-intercepts", and you'll be able to answer the question, even though they never gave you the equation.
URL: https://www.purplemath.com/modules/intrcept.htm
You can use the Mathway widget below to practice finding intercepts. Try the entered exercise, or type in your own exercise. Then click the button and select "Find the x and y Intercepts" to compare your answer to Mathway's.
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()