The Purplemath Forums
Helping students gain understanding
and self-confidence in algebra

Converting Between Decimals,
     Fractions, and Percents (page 3 of 4)

Sections: Percent to Decimal, Percent to Fraction, Decimal to Fraction, Decimal to Percent,
               Fraction to Decimal, Fraction to Percent, Tables of Equivalents

Fraction to Percent

This conversion starts the same as the previous one, but the final answer can come in a couple different formats sometimes. You always start by doing the division (fractions are division, remember!), and then (usually) you move the decimal point two places to the right. For example:

However, sometimes the "decimal expansion" doesn't end. This is where the answer can come in a couple different formats. You can either round the answer, or use a fraction inside the percent. For instance:   Copyright © Elizabeth Stapel 2006-2008 All Rights Reserved

You can round this to, say, 0.389 = 38.9%. But if you aren't supposed to round, put out a sheet of paper and do the long division. You'll need to get TWO decimal places of answer across the top, and then look at the remainder at the bottom:

Fractions are division, so I took the 7and divided by the 18. I kept going until I had TWO decimal places (the ".38") across the top. At that point, the remainder is 16. If you think back to elementary school, you handle the remainder by putting it over the divisor (18, in this case), and tacking it on to the number across the top. In this case, I get:

So ⁷/₁₈, expressed as an unrounded decimal, is 38 ⁸/₉%. This probably looks a little weird, so let's do a couple more examples. For instance, other than memorizing, how are you supposed to know that 0.333333... = ¹/₃? Here's how:

This doesn't end, so do the long division by hand:

Note that the remainder is 1 and the divisor is 3, so you'll be tacking a " ¹/₃ " on to the "0.33" from the top:

Here's a messier example that you won't have memorized:

This doesn't end, so do the long division by hand:

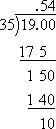
Note that the remainder is 10 and the divisor is 35, so you'll be tacking a " ¹⁰/₃₅ " on to the "0.54" from the top:

<< Previous  Top  |  1 | 2 | 3 | 4  |  Return to Index  Next >>

  Copyright © 1999-2010  Elizabeth Stapel   |   About   |   Terms of Use

 Feedback   |   Error?