The Purplemath Forums
Helping students gain understanding
and self-confidence in algebra

Converting Between Decimals,
     Fractions, and Percents (page 2 of 4)

Sections: Percent to Decimal, Percent to Fraction, Decimal to Fraction, Decimal to Percent,
               Fraction to Decimal, Fraction to Percent, Tables of Equivalents

Decimal to Fraction

The technique I just demonstrated lets you convert any terminating decimal to a fraction.

("Terminating" means "it ends", unlike, say, the decimal for ¹/₃, which goes on forever. A non-terminating AND NON-REPEATING decimal CANNOT be converted to a fraction, because it is an "irrational" (non-fractional) number. You should probably just memorize some of the more basic repeating decimals, like 0.33333... = ¹/₃ and 0.666666... = ²/₃. Check out the table on the last page.)

Any terminating decimal can be converted to a fraction by counting the number of decimal places, and putting the decimal's digits over 1 followed by the appropriate number of zeroes. For example:

In the case of a repeating decimal, the following procedure is often used. Suppose you have a number like 0.5777777.... This number is equal to some fraction; call this fraction "x". That is:

x = 0.5777777...

There is one repeating digit in this decimal, so multiply x by "1" followed by one zero; that is, multiply by 10:

10x = 5.777777...

Now subtract the former from the latter:

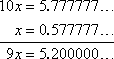
That is, 9x = 5.2 = 52/10 = 26/5. Solving this, we get x = 26/45. (You can verify this by plugging "26 ÷ 45" into your calculator and seeing that you get "0.5777777..." for an answer.)

If there had been, say, three repeating digits (such as in 0.4123123123...), then you would multiply the x by "1" followed by three zeroes; that is, you would multiply by 1000. Then subtract and solve, as in the above example. And don't worry if you have leading zeroes, as in "0.004444..."; the procedure will still work.

Decimal to Percent

Decimal-to-percent conversions are simple: just move the decimal point two places to the right. (Remember, $0.50 is one-half, or 50%, of a dollar.) For example:

0.23 = 23%
2.34 = 234%
0.0097 = 0.97%

(Note that 0.97% is less than one percent. It should not be confused with 97%, which is 0.97 as a decimal.)

Fraction to Decimal

If you remember that fractions are division, then this is easy. The calculator can do the work for you, because you can just have it do the division. For example:

The bar is placed over the repeating digits, for convenience sake.

When converting fractions to decimals, you may be told to round to a certain place or to a certain number of decimal places. For instance, looking at that last example, ²/₇ as a decimal rounded to the nearest tenth (rounded to one decimal place) is 0.3; to the nearest hundredth (to two decimal places) is 0.29; to the nearest thousandths (to three decimal places) is 0.286; to the nearest ten-thousandths (to four decimal places) is 0.2857; et cetera. If you're not sure how you should format your answer, then give the "exact" form and the rounded form:

Note that the rounded form can be useful for word problems, where a final answer in rounded form may be more practical than a repeating decimal.

<< Previous  Top  |  1 | 2 | 3 | 4  |  Return to Index  Next >>

  Copyright © 2010  Elizabeth Stapel   |   About   |   Terms of Use

 Feedback   |   Error?