Function Reflections
Purplemath
What is a function reflection (in math)?
A function reflection is the graph of the original function, but where the graph has been flipped upside-down (that is, where it has been "reflected in the x-axis") or where it has been mirrored (that is, where it has been "reflected in the y-axis).
Content Continues Below
How do you write a reflective function?
To write a reflective function, multiply either the variable x or else the function name by −1. The graph of the function g(−x) is the same as the graph for g(x), but has been rotated around the y-axis; the graph of −g(x) is the same as the graph for g(x), but has been rotated around the x-axis.
What are the rules for function reflection?
The two rules for function reflection are these:
- To reflect the graph of a function h(x) over the x-axis (that is, to flip the graph upside-down), multiply the function by −1 to get −h(x).
- To reflect the graph of a function h(x) around the y-axis (that is, to mirror the two halves of the graph), multiply the argument of the function by −1 to get h(−x).
What is an example of function reflection?
To see how function reflection works, let's take a look at the graph of h(x) = x2 + 2x − 3. The graph of the original function looks like this:
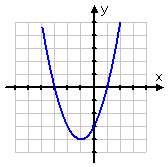
To picture this graph flipping upside-down, imagine that the graph has been drawn on a sheet of clear plastic that has been placed over a drawing of just the y-axis, and that the x-axis is a skewer that has been stuck through the sheet. To flip the graph, turn the skewer 180°. (Pictures here.) Then the new graph, being the graph of −h(x), looks like this:
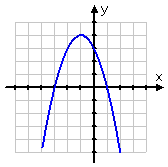
Flipping a function upside-down always works this way: you slap a "minus" on the whole thing. The "flipping upside-down" thing is, slightly more technically, a "mirroring" of the original graph in the x-axis. If you think of taking a mirror and resting it vertically on the x-axis, you'd see (a portion of) the original graph upside-down in the mirror. When they talk about "mirroring" or "reflecting" in or about an axis, this is the mental picture they have in mind.
To keep straight what this transformation does, remember that f (x) is the exact same thing as y. So, by putting a "minus" on everything, you're changing all the positive (above-axis) y-values to negative (below-axis) y-values, and vice versa.
Important to know: Any points on the x-axis stay right where they are when you reflect the function's graph over the axis. It's only off-axis points that move.
Content Continues Below
The previous reflection was a reflection in the x-axis. This leaves us with the transformation for doing a reflection in the y-axis.
For this transformation, I'll switch to a cubic function, being g(x) = x3 + x2 − 3x − 1.
Here's the graph of the original function:
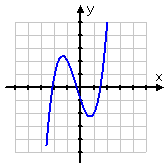
If I put −x in for x in the original function, I get:
g(−x) = (−x)3 + (−x)2 − 3(−x) − 1
= −x3 + x2 − (−3x) − 1
= −x3 + x2 + 3x − 1
This new function graphs like this:
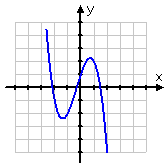
This transformation rotated the original graph around the y-axis. Any points on the y-axis stay on the y-axis; it's the points off the axis that switch sides. This is always true: g(−x) is the mirror image of g(x); plugging in the "minus" of the argument gives you a graph that is the original graph, but reflected in the y-axis.
Affiliate
To keep straight what this transformation does, remember that you're swapping the x-values. Whatever you'd gotten for x-values on the positive (or right-hand) side of the graph, you're now getting for x-values on the negative (or left-hand) side of the graph, and vice versa. Since the inputs switched sides, so also does the graph.
What is an example of function reflection?
-
Given the graph below of a function f (x), determine which of Graphs A and B represent f (−x) and −f (x).
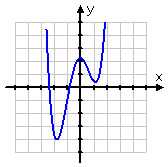
They've given me Graph A:
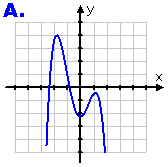
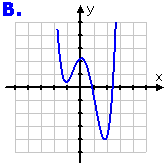
...and Graph B:
Comparing Graphs A and B with the original graph, I can see that Graph A is the upside-down version of the original graph. It's been reflected across the x-axis. This means that it's the "minus" of the original function; it's the graph of −f (x).
Graph B has its left and right sides swapped from the original graph; it's been reflected across the y-axis. That means that this is the "minus" of the function's argument; it's the graph of f (−x).
Graph A represents −f (x)
Graph B represents f (−x)
Affiliate
-
Given the function f (x) = x2 + x − 3, find the function statements, in simplified form, for the reflection of the function in each of the x- and y-axes. Label the reflections appropriately.
Well, "appropriately" is a little vague; I'll just be sure the label everything very clearly.
Affiliate
I need to find the simplified functional statements for each of the reflections. One of the reflections involves putting a "minus" on the function; the other involves putting a "minus" on the argument of the function. So I'll do each of these.
First up, I'll put a "minus" on the argument of the function:
f (−x) = (−x)2 + (−x) − 3
= x2 − x − 3
Now for the other reflection:
−f (x) = −(x2 + x − 3)
= −x2 − x + 3
Putting a "minus" on the argument reflects the graph in the y-axis. Putting a "minus" on the whole function reflects the graph in the x-axis. So my (clearly labelled) answer is:
reflection in the y-axis:
f (−x) = x2 − x − 3
reflection in the x-axis:
−f (x) = −x2 − x + 3
Many textbooks don't get any further than this. If these are all the rules you need, then write 'em down and make sure you've done enough practice to be able to keep them straight on the next test:
The function translation / transformation rules:
- f (x) + b shifts the function b units upward.
- f (x) − b shifts the function b units downward.
- f (x + b) shifts the function b units to the left.
- f (x − b) shifts the function b units to the right.
- −f (x) reflects the function in the x-axis (that is, upside-down).
- f (−x) reflects the function in the y-axis (that is, swapping the left and right sides).
URL: https://www.purplemath.com/modules/fcntrans2.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()