Function Translations
Purplemath
What is "function translation"?
One definition of "to translate" is "to change from one place, state, form, or appearance to another". When we take a function and tweak its rule so that its graph is moved to another spot on the axis system, yet remains recognizably the same graph, we are said to be "translating" the function.
Content Continues Below
How do you translate functions (in math)?
To translate a function, you add or subtract inside or outside the function. The four directions in which one can move a function's graph are up, down, to the right, and to the left.
Usually, translation involves only moving the graph around. Squeezing or stretching a graph is more of a "transformation" of the graph. But these two topics are usually taught at the same time, and usually under the same name. Just be aware that the topic of "function translation" often includes function transformation, and vice versa.
To get started, let's consider one of the simpler types of functions that you've graphed; namely, quadratic functions and their associated parabolas.
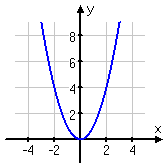
When you first started graphing quadratics, you started with the basic quadratic:
f (x) = x2:
Then you did some related graphs, such as:
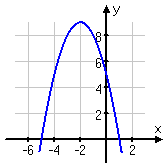
g(x) = −x2 − 4x + 5:
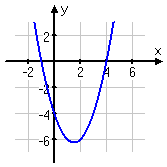
h(x) = x2 − 3x − 4:
k(x) = (x + 4)2:
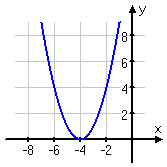
In each of these cases, the basic parabolic shape was the same. The only difference was where the vertex was, and whether the parabola was right-side up or upside-down.
If you've been doing your graphing by hand, you've probably started noticing some relationships between the equations and the graphs. The topic of function translation makes these relationships more explicit.
Content Continues Below
How do you translate a function up or down?
To translate a function's graph upward or downward, add or subtract (respectively) from the original function. For instance, given g(x), adding 3 to the formula for g moves the graph of g three units upward; that is, the graph of g(x) + 3 is the same as the graph of g(x), but it moved upward by 3.
To see what this looks like, let's start with the function notation for the basic quadratic:
f (x) = x2
A function transformation takes whatever is the basic function f (x) and then "transforms" it (or "translates" it), which is a fancy way of saying that you change the formula a bit and thereby move the graph around.
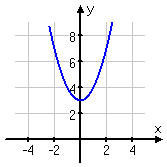
For instance, the graph for y = x2 + 3 looks like this:
Advertisement
Affiliate
This parabola is three units higher than the basic quadratic's graph, f (x) = x2; specifically, x2 + 3 is f (x) + 3. We added a 3 outside the basic squaring function f (x) = x2 and thereby went from the basic quadratic x2 to the transformed function x2 + 3.
This is always true: To move a function up, you add outside the function: f (x) + b is f (x) moved up by b units. Moving the function down works the same way, but by adding a negative number (or, which is the same thing, subtracting a positive number); f (x) − b is f (x) moved down by b units.
- Given g(x) = 4x − 3, what function h(x) would represent a downward shift by two units?
They're wanting me to move the original function downward by two units. To make this happen, the new function is going to be the old one, but with a "minus two" tacked onto the end (and then I'll simplify, if possible).
g(x) − 2 = (4x − 3) − 2
= 4x − 5
Then the new function is:
h(x) = 4x − 5
How do you move a function left or right?
We can move functions (and their associated graphs) to the left and to the right by adding or subtracting, respectively, inside the function. For instance, y = (x + 3)2 looks like this:
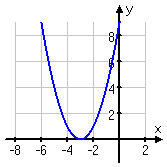
In this graph, f (x) has been moved over three units to the left: f (x + 3) = (x + 3)2 is f (x) shifted three units to the left.
This is always true: To shift a function left, add inside the function's argument: f (x + b) gives f (x)shifted b units to the left. Shifting to the right works the same way; f (x − b) is f (x) shifted b units to the right.
Warning: The common temptation is to think that f (x + 3) moves f (x) to the right by three, because "+3" is to the right. But the left-right shifting is backwards from what you might have expected.
Adding moves you to the left; subtracting moves you to the right.
If you lose track, think about the point on the graph where x = 0. For f (x + 3), what does x now need to be for 0 to be plugged into f ? In this case, x needs to be −3, so that the argument becomes −3 + 3 = 0. This tells me that I need to shift left by three.
This process — of figuring out how to get zero inside a function's argument — will tell you how the x-values, and thus the graph, have shifted. At least, that's how I was able to keep track of things. Yes, I had trouble with this concept, too.
- Given f (x) = −x2 + 5x + 2, find the expression, in terms of f , for a leftward shift of five units.
To shift the graph side to side, I need to add or subtract inside the argument of the function (that is, inside the parentheses). To move to the left, I (counter-intuitively) need to add inside the parentheses. To move five units, I'll need to add 5 inside the parentheses.
Then my answer is:
f (x + 5)
- Given s(t) = 2t + 4, find the expression for the function w(t) which represents a rightward shift of one unit of s(t).
Affiliate
They've told me to shift to the right. To do this, I must (counter-intuitively) subtract inside the argument. They've told me to shift rightward by one unit, so I'll be subtracting by 1.
But they haven't told me to express the new function in terms of the old. They want the actual expression for the rightward shift. So I'll need to do some algebra, plugging in a "t − 1" for every instance of "t " in the original function. Fortunately, that function is really simple, so:
w(t) = s(t − 1)
= 2(t − 1) + 4
= 2t − 2 + 4
= 2t + 2
Then my new function is:
w(t) = 2t + 2
To sum up, the four rules for function translations are these:
- To move a graph upward, add to the function; for example, f (x) + 2 moves the graph of the function f (x) upward by 2 units.
- To move a graph downward, subtract from the function; for example, f (x) − 3 moves the graph of the function f (x) downward by 3 units.
- To move a graph to the right, subtract from the argument of the function; for example, f (x − 4) moves the graph of the function f (x) rightward by 4 units.
- To move a graph to the left, add to the argument of the function; for example, f (x + 5) moves the graph of the function f (x) leftward by 5 units.
URL: https://www.purplemath.com/modules/fcntrans.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()