Moving Points
Purplemath
Sometimes you'll be given a point, or a graph with clearly-plotted points, and you'll be told to translate the point(s) according to some rule. In other words, they won't be giving you a function (complete with the function's formula) to move (so you won't be able to use your graphing calculator to check your work); instead, you'll be given points to move, and you'll have to know how to flip them around the axis system yourself.
Content Continues Below
Here's an example of what that looks like:
-
Given the following graph of f (x), graph the transformation −f (x + 1) − 3
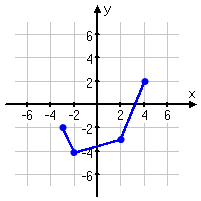
This transformation formula has just about everything: there's a left-shift of one (being the "+1" inside the argument of the function), a move-down by three (being the "−3" outside the function), and a flip-upside-down (eeing the "minus" sign multiplied onto the function directly). And, worse yet, I have no formula for f (x), so I can't cheat; I have to do the transformation myself, point by point.
The way the original graph is drawn, there are four clearly-plotted points that I can use to keep track of things.
(In situations like this, they must give you clearly-plotted points, either labelled with coordinates or else obviously at integer x- and y-values. Otherwise, there's no reasonable way for you to locate any points. So if, in an exercise like this, a point looks like it has nice neat coordinate values, you can safely assume that it does indeed have those nice values.)
If I move the plotted points successfully, then I can fill in the rest of the graph once I'm done.
Affiliate
Note: What I'm going to show you below is not what you would hand in. You would not show all this work in your homework, and certainly not on a test. But this displays the thinking that should be going through your head as you transform each point. If you're not sure of yourself, this might be what your scratch-paper would look like.
I'll work on the points in order, moving from left to right.
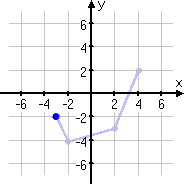
The first point I'll work with is the point (−3, −2). I've highlighted this point in blue, above.
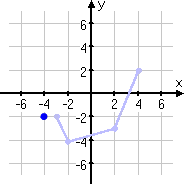
First, I'll do the inside-the-argument change, and shift the point left by one unit, to its new location of (−4, −2).
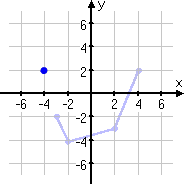
Next, I'll do the negative-of-the-function change, and flip the point over the x-axis, up to (−4, 2).
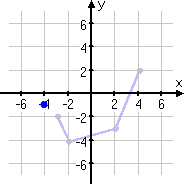
Finally, I'll do the subtracted-outside-the-function change, and move the point down three units, to (−4, −1). This is the first point's new (translated) location.
That's the first point. Now I'll work on the second point from the left.
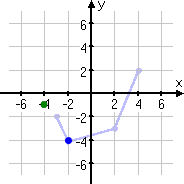
The next point is (−2, −4).
(The previous point is shown in its new location, in green. Colored pencils can be helpful for this sort of thing.)
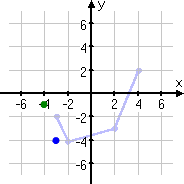
I'll move the point back to the left by one unit, to (−3, −4).
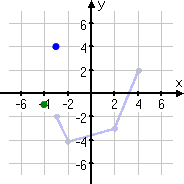
Flipping this point across the x-axis moves the point to (−3, 4).
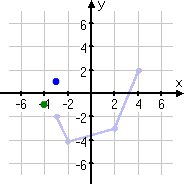
Moving the point three units down takes it to (−3, 1). This is the second point's new (translated) location.
Content Continues Below
On now to the third of the original points. (The second point is shown on the graph below in green, to highlight its new location.)
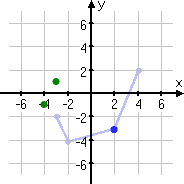
The third point I'll move is at (2, −3).
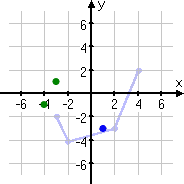
Shifting to the left by one takes the point to (1, −3).
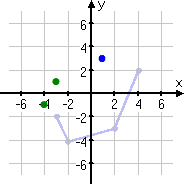
Flipping this point across the x-axis takes the point to (1, 3).

Moving the point down three units takes it to (1, 0), on the horizontal axis.
Three points down; one to go.
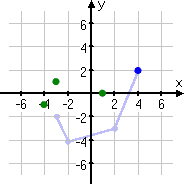
The last point that I need to move is (4, 2).
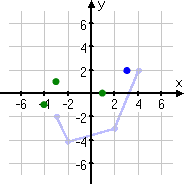
Shifting the point one unit to the left takes it to (3, 2).
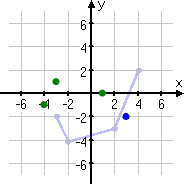
Flipping across the x-axis takes the point to (3, −2).
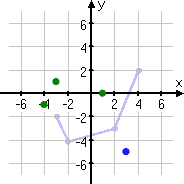
Moving the point three units down takes it to (3, −5).
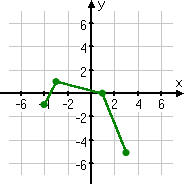
Now that I've moved all the points, I can graph the transformation.
Affiliate
If you're not sure of the order in which to do the transformation's steps, then stick to working from the inside out (from inside the argument, to anything that's multiplied onto the function, to anything done outside the function), like I did above. Figure out the exact sequence of steps that each point will need to make. Then pick a point to move, and trace out the sequence of steps with your pencil tip, drawing in the translated point once you reach its final location. Then, once you've moved all of the points, you can draw in the transformation.
Note: For the above transformation, they could have factored the minus sign from out in front of the translation expression, and then presented the transformation to me as being −[ f (x + 1) + 3 ]. Then the point movements would have been "left one, up three, and then flip across the x-axis". But the end result would have been exactly the same.
(It can be helpful to use a pencil [say, on the test] to trace the moving points. Once you get a point's final transformed location, you can erase the pencilled in-between steps.)
If your book or instructor uses this other way of expressing transformations, or if you get an exercise that's formatted this way, don't panic. Just work things out logically and step-by-step — and, if you prefer, multiply things back out to get a transformation expression more like what we'd started this page with.
URL: https://www.purplemath.com/modules/fcntrans4.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()




