Symmetry About an Axis
Purplemath
"Symmetry" is a recognition of the matching-ness of the parts of a shape.
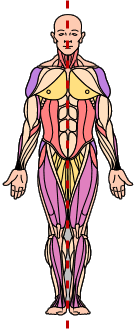
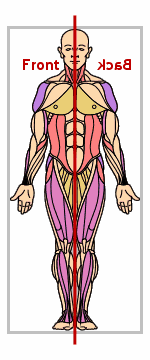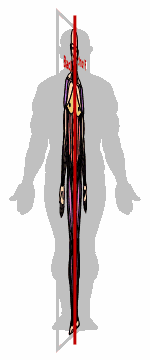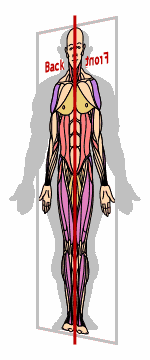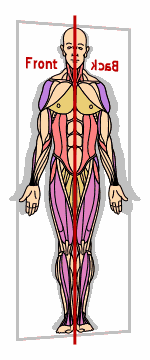
For instance, the human body is said to have "bilateral" (that is, two-sided) symmetry, because the left and right halves of the body mirror each other externally, as you can see in the image below:
Content Continues Below
But this symmetry applies only to the basic framing structure of our bodies; much of our insides, our organs, don't match, as you can see in the image to the right: watch the liver (brown) and the stomach (pink) change sides when the organs are flipped.:
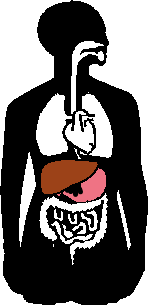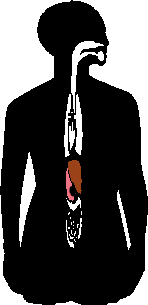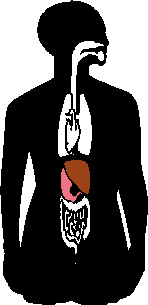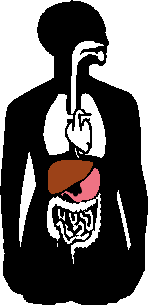
(The above graphic is animated on the "live" site.)
The dotted line running down the middle of the first graphic above is called "the axis of symmetry".
If you think of the bilateral-symmetry picture as being drawn on a sheet of transparent plastic with a shish-kebob skewer punched through the dotted line, you could twirl the skewer (and thus the sheet) 180° around and end up looking at the same picture, but from the other side of the plastic sheet:
(The above graphic is animated on the "live" site.)
A figure has as many symmetries as its plastic sheet can have skewers.
For instance, a rectangle can be twirled through its middles, so a rectangle has two symmetries.

(The above graphic is animated on the "live" site.)
A square can also be twirled along its diagonals, so a square has four symmetries.

(The above graphic is animated on the "live" site.)
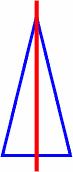
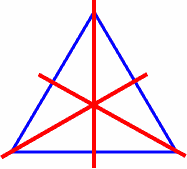
A triangle might have one or three lines of symmetry, but usually has none. For instance:
one line of symmetry:
three lines of symmetry:
no lines of symmetry:

And a circle has infinitely-many lines of symmetry, since any line through its center (that is, any diameter) is also an axis of symmetry.
Content Continues Below
When working with symmetry about a line, you'll usually be asked for symmetry about an axis. With parabolas (and other conics), you may be asked for symmetry about any line. Either way, the concepts are the same, because:
The x-axis is just the line y = 0, and the y-axis is just the line x = 0.
Here are some examples of these types of symmetry:
The parabola y = x2 − 4 is shown below:
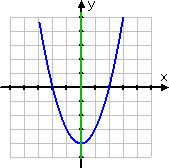
The line (or "axis") of symmetry is the y-axis, also known as the line x = 0. This line is marked green in the picture. The graph is said to be "symmetric about the y-axis", and this line of symmetry is also called the "axis of symmetry" for the parabola.
Contrary to the previous example, the parabola y = (x − 2)2 − 4 has a line (or axis) of symmetry, but is not symmetric about either axis (that is, it is not symmetric about the x- or y-axis):
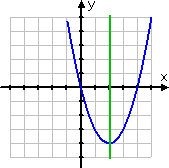
The axis here is the line x = 2, as marked in green above. If you were asked to "find the axis of symmetry for the parabola", you would answer "x = 2".
Affiliate
However, if you were asked, "Is the graph symmetric about either axis?", you would understand them to be asking only about symmetry about either the x- or y-axis; you would answer, "No."
Sometimes, you'll be asked about the symmetry of graphs which do not correspond to functions, but are actually relations. (That is, the graphs don't pass the Vertical Line Test.) Non-functional relations can have axes of symmetry. For instance, the graph of y2 = x + 4 is symmetric about the x-axis:
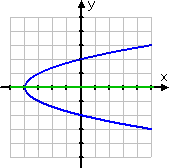
The axis of symmetry is the line y = 0, which is also the x-axis. If you were asked if this graph is symmetric about either axis, you would say, "Yes; about the x-axis." If you were asked for the axis of symmetry of the (sideways) parabola, you would say, "the line y = 0."
On the other hand, the shifted parabola given by (y − 2)2 = x + 4 has an axis of symmetry, but it is not symmetric about either of the (regular) axes:
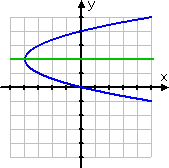
If you were asked, "Is this graph symmetric about either axis?", you would answer, "No." If you were asked for the axis of symmetry, you would reply with "y = 2" or "the x-axis."
Affiliate
In other words, you answer will vary with the context. If you're finding "even" functions, you'll be looking at one sort of symmetry (that is, symmetry about the y-axis). If you're looking at the graphs of conics, you'll be looking at a different sort of symmetry (that is, symmetry about any straight line, usually being parallel to one of the x- and y-axes).
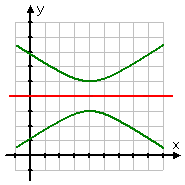
By the way, don't let the preceding graphs fool you. The line of symmetry need not pass through or touch the graph of the underlying function or relation. For instance, the axis of symmetry for an hyperbola will not touch the graph:
horizontal line of symmetry:
not touching the hyperbola
URL: https://www.purplemath.com/modules/symmetry.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()