Symmetry about a Point

The Purplemath Forums
Helping students gain understanding
and self-confidence in algebra

Return to the Lessons Index | Do the Lessons in Order | Get "Purplemath on CD" for offline use | Print-friendly page

Symmetry about a Point (page 2 of 3)

Sections: Symmetry about an axis, Symmetry about a point, Symmetry and graphing

In addition to finding lines (axes) of symmetry, you can also look for points of symmetry.

A point of symmetry is a point that represents a "center" of sorts for the figure. For any line that you draw through the point of symmetry, if this line crosses the figure on one side of the point, the line will also cross the figure on the other side of the point, and at exactly the same distance from the point

For instance, a figure-eight has a point of symmetry in the middle, where the lines cross (shown by the blue dot):

a figure-8, showing symmetry about the center

For an hyperbola, the center is the point of symmetry:

As you can see from the hyperbola, a point of symmetry doesn't have to be a point on the figure; it can lie outside the figure or graph; in this case, the point of symmetry happens to be the origin.

an hyperbola, showing its point of symmetry

You can also view points of symmetry as being points about which you can rotate the shape 180°, as shown below.

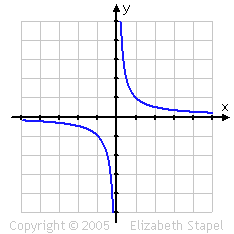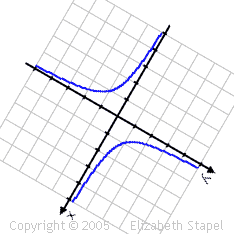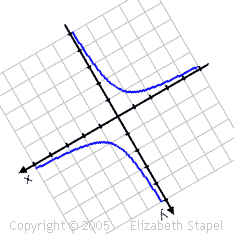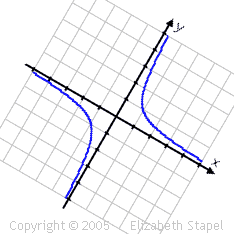
an hyperbola, rotating about its point of symmetry

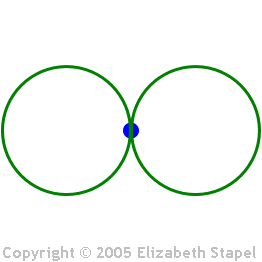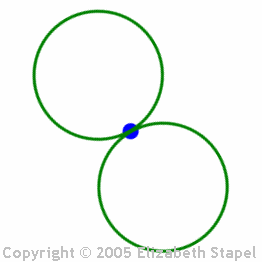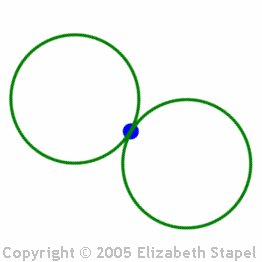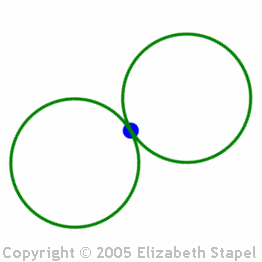
a figure-8, rotating about its point of symmetry

Axes and points of symmetry can be anywhere on the plane. Points of symmetry do not have to be the origin; lines of symmetry do not have to correspond to either axis.

point of symmetry: not at the origin		line of symmetry: not along either axis

The points and lines of symmetry do not even have to touch the figure, and lines of symmetry do not have to be vertical:

point of symmetry: not on the ellipse		horizontal line of symmetry: not touching the hyperbola

It should be noted, however, that the lines of symmetry for the ellipse and the vertical line of symmetry for the hyperbola will touch their respective figures. Whether or not particular lines and points of symmetry will touch their figures will vary from figure to figure.

<< Previous Top | 1 | 2 | 3 | Return to Index Next >>

Cite this article as:

Stapel, Elizabeth. "Symmetry about a Point." Purplemath. Available from
http://www.purplemath.com/modules/symmetry2.htm. Accessed

Purplemath:
  Linking to this site
  Printing pages
  Donating
  School licensing

Reviews of
Internet Sites:
   Free Help
   Practice
   Et Cetera

The "Homework
Guidelines"

Study Skills Survey

Tutoring ($$)

This lesson may be printed out for your personal use.

Copyright © 2005-2009 Elizabeth Stapel \| About \| Terms of Use		Feedback \| Error?