The Unit Circle
Purplemath
When you work with angles in all four quadrants, the trig ratios for those angles are computed in terms of the values of x, y, and r, where r is the radius of the circle that corresponds to the hypotenuse of the right triangle for your angle. In the drawing below, the angle ends in the second quadrant, as indicated by the diagonal-ish line:
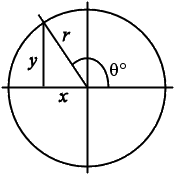
Content Continues Below
Any two right triangles with the same base angle θ ("theta", pronounced THAY-tuh) will be similar in the technical sense of having their sides in proportion. This similarity is more obvious when when the triangles are nested:
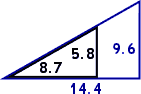
Similarity (and thus proportionality) means that the trig ratios from the two nested triangles displayed above will be the same, as you can see from the computations below for each of the two triangles above:
small (black) triangle:
large (blue) triangle:
The trig ratios for the same-sized angle θ are the same (as you can see above), even though the specific numbers from the two triangles' sets of sides are different. This emphasizes that, for trigonometric ratios, it's the angle θ that matters, not the particular triangle from which you obtained that angle.
To simplify computations, mathematicians like to fit an angle's triangle into a circle with radius r = 1. Because the number 1 is called "the unit" in mathematics, a circle with a radius of length 1 is called "the unit circle". Once the hypotenuse has a fixed length of r = 1, then the values of the trig ratios will depend only on x and y, since multiplying or dividing by r = 1 won't change anything. Only the values of x and y will matter.
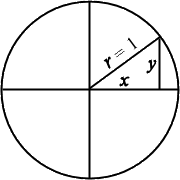
Content Continues Below
The Unit Circle
The point of the unit circle is that it makes other parts of the mathematics easier and neater. For instance, in the unit circle, for any angle θ, the trig values for sine and cosine are clearly nothing more than sin(θ) = y and cos(θ) = x. Working from this, you can take the fact that the tangent is defined as being tan(θ) = y/x, and then substitute for x and y to easily prove that the value of tan(θ) also must be equal to the ratio sin(θ)/cos(θ).
Another thing you can see from the unit circle is that the values of sine and cosine will never be more than 1 or less than −1, since x and y never take on values outside of this interval. Also, since tangent involves dividing by x, and since x = 0 when you're one-fourth and three-fourths of the way around the circle (that is, when you're at 90° and at 270°), the tangent will not be defined for these angle measures.
Certain angles have "nice" trig values. These angles, in the first quadrant (being the "reference" angles) are 0°, 30°, 45°, 60°, and 90°. (Strictly speaking, 0deg and 90deg aren't "in" any quadrant, but we'll work with them as though they were in the first quadrant. It's just easier that way.) So you'll probably be expected to have memorized the trig-function values for these angles. You'll probably now also be provided with a circle, having those angles marked. In the first quadrant, we have the following:
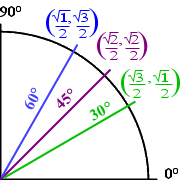
(You may have noticed the radicals on the 1's in the above. Yes, these simplify to just 1, so you can write things that way, too, and you certainly should do the simplification in your final hand-in answer. But notice how all the denominators are 2's, and how the numerators go up or go down, 1, 2, 3. This can be helpful for remembering the trig values.)
Affiliate
You might be given a complete unit circle, with the values for the angles in the other three quadrants, too. But you only need to know the values in the first quadrant. Once you know them, and because the values repeat (other than sign) in the other quadrants, you know everything you need to know about the unit circle.
Affiliate
-
Confirm that the point is a point on the unit circle. Find the sine and cotangent of the angle A having this point on its terminal side.
Any point on the unit circle will be a distance of one unit from the center; this is the definition of the unit circle. To "confirm" that the point they've given me is a point on the unit circle, I can apply the Pythagorean Theorem to find the length of the radius of the right triangle formed by dropping a perpendicular from the x-axis down to the point. My perpendicular is the bright blue dashed line:
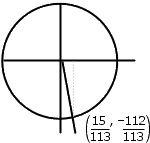
If the Pythagorean Theorem gives me a value for the radius of 1, then I'll have "confirmed" that the point is on the unit circle.
Then the length of the third side of the right triangle, which is also the length of the radius of the circle, is 1. So this point is indeed on the unit circle.
Now they want me to find the sine and cotangent of the underlying angle. The sine is the y-value. (I don't need to worry about the hypotenuse, because it's always 1 in the unit circle.) So the sine of the underlying angle is:
The cotangent is the reciprocal of the tangent. The tangent is "opposite over adjacent" or, in this context, "y over x". Then the cotangent is the reciprocal of this:
My answer for the first part of this exercise was where I showed that the radius equalled 1. The rest of my hand-in answer is:
URL: https://www.purplemath.com/modules/unitcirc.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()



