The Pythagorean Theorem
Purplemath
Back when you first studied square roots and how to solve radical equations, you were probably introduced to something called "the Pythagorean Theorem". This Theorem relates the lengths of the three sides of any right triangle.
This Theorem existed way before Pythagorus and his followers, the Pythagoreans, by the way.
Content Continues Below
To set things up, let's consider right triangles. A right triangle is a triangle in which one of the angles measures 90°. The two shorter sides of the triangle, being the two sides that meet at the right angle of the triangle, are called the "legs" of the triangle, and are customarily labelled as having lengths a and b; the long side of the triangle, which is opposite the right angle, is called the "hypotenuse", and is customarily labelled as having length c. These variables, in modern analytic geometry, are used in the Pythagorean Theorem.
What is the Pythagorean Theorem?
Affiliate
Advertisement
The Pythagorean Theorem is a rule that relates the two legs of a right triangle, having lengths a and b, to the length c of the hypotenuse by the following rule:
a2 + b2 = c2
This equation allows you to find the length of a side of a right triangle when they've given you the lengths for the other two sides, and, going in the other direction, allows you to determine if a triangle is a right triangle when they've given you the lengths for all three sides.
- Given the right triangles (a) and (b) displayed below, find the lengths of their remaining sides.
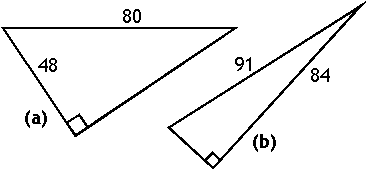
They've given me two triangles, named (a) and (b). I'll label my work and answers accordingly.
(a) The side opposite the right angle is c; how I name the other two sides really doesn't matter. I'll plug the values into the Theorem, and solve:
802 = 482 + b2
6400 = 2304 + b2
4096 = b2
±64 = b
64 = b
Affiliate
Normally when solving a quadratic equation like this, I'd need both answers, from the ± due to taking the square root of either side. In this case, though, I am looking for a lengths, so I knew going in that I would be needing to find a positive value for the length of the third side. This is why I could ignore the negative solution.
Then the length of the leg is given by:
triangle (a): b = 64
(b) This triangle one works the same way as did (a):
912 = 842 + b2
8281 = 7056 + b2
1225 = b2
±35 = b
35 = b
Again, because I'm looking for a length which cannot be negative, I can ignore the negative square root. My answer must be positive:
triangle (b): b = 35
When dealing with dimensions like lengths, we are typically also dealing with units, such as meters or inches. But they didn't put any units either in the exercise statement or in the drawing, so my answers had to be just the plain numbers.
In real life, of course, this would not fly. Units matter.
Content Continues Below
- Given the triangles below, determine if the triangles are right triangles.

They have labelled the two triangles as (a) and (b). I will label my work and my answers accordingly.
{a) I need to see if the squares of the legs equal the square of the hypotenuse:
452 + 552 = 2025 + 3025 = 5050
752 = 5625
The sum of the squares of the lengths of the two legs is 5,050, while the square of the length of the hypotenuse is 5,625. These are not equal. Therefore:
triangle (a) is NOT a right triangle
(b) This one works the same as for (a):
282 + 452 = 784 + 2025 = 2809
532 = 2809
The sum of the squares of the lengths of the two legs is 2,809, and the square of the length of the hypotenuse is also 2,809. These are equal, so:
triangle (b) is a right triangle
URL: https://www.purplemath.com/modules/pythagthm.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()