Solving Radical Equations: Concepts

In general, we solve equations by isolating the variable; that is, we manipulate the equation to end up with the variable on one side of the "equals" sign, with a numerical value on the other side. The general process for isolation is, in a sense, undoing whatever had been done to the variable in the original equation.

For instance, suppose we are given the following linear equation:

To solve, we would undo the addition of the 2; that is, we'd subtract the 2 over to the other side of the equation:

On the other hand, given the equation −3x = 12, we would solve by undoing the multiplication; that is, we would divide through by −3:

When we have a variable inside a square root, we undo the root by doing the opposite; that is, we square both sides of the equation. For instance, given the equation , we would solve by squaring both sides of the equation:

Before we dive into worked examples, we need to discuss a couple of issues.

---

Issue 1: Square Sides, not Terms

When solving an equation, we must do the same thing to both sides of the equation; in particular, we don't do things to each term in the equation. In the first example above, when solving "x + 2 = 5", I subtracted a 2 from each side, not from all three terms.

When solving a radical equation, we must square both sides; we should never try to square every term. For example, I can start with a true equation:

...and then square both sides:

By squaring both sides of the equation, I end up with a true equation. That's how the math is supposed to work. But if I try squaring the terms on the left-hand side of the original statement above, I won't end up with the correct value.

Obviously, this is wrong.

In each case, I'd started with a true statement. When I squared both sides of that true statement, I ended with a true statement. But when I squared the terms on the left-hand side, I ended up with an untrue statement: "25 =49".

The most common mistake when solving radical equations is trying to square terms. Always square sides, not terms.

---

Issue 2: Check Your Answers

We can always check our solution to an equation by plugging that solution back into the original equation and making sure that it results in a true statement. For instance, in my first example above, "x + 2 = 5", I got a solution of x = 3. I can confirm this solution by plugging it back into the original equation:

You probably did this type of checking back when you first learned about solving linear equations. But eventually you honed your skills, and you quit checking.

The difficulty with solving radical equations is that we may do every step correctly, but still end up with a wrong answer. This is because the very act of squaring the sides can create solutions that never existed before. For instance, I could claim the following:

This is nonsense, of course. But look what happens when I square both sides:

I started with something that was not true, squared both sides of it, and ended with something that was true. This is not good.

Squaring both sides of an equation is an "irreversible" step, in the sense that, having taken the step, we can't necessarily go back to what we'd started with. By squaring, we may have lost some of the original information. (This is just one of many potential errors possible in mathematics.)

To see how this works in our current context, let's look at a very simple radical equation:

This equation is no more true than was the "−2 = 2" nonsense we looked at previously, and it's nonsense for the exact same reason: no positive value (in this case, a square root) can ever equal a negative number.

But suppose I hadn't noticed that this equation can't possibly have any solution, and had instead proceeded mindlessly to square both sides:

By squaring both sides, I got rid of the problemmatic "minus" sign, magically creating a solution which had not previously existed and is in fact not valid. But I won't discover this error unless I remembered to check my solution! Plugging my solution value into the left-hand side of the original equation, I check to see if I get the required value of the original right-hand side:

Now I can clearly see that something is amiss. I can't have a negative number equal to a positive number. Now I can see that the actual answer for this equation is:

---

There is another way to look at this "no solution" difficulty. When we are solving an equation, we can view the process as trying to find where two lines intersect on a graph. The left-hand side of the equation can be graphed as one curve, and the right-hand side of the equation can be graphed as another curve. The solution to the original equation is the intersection of the two curves. (Yes, this means that you can use your graphing calculator to help you check your work.)

When I was solving "x + 2 = 5" above, you could also say that I was trying to find the intersection of the two curves:

The graph shows where these two lines intersect:

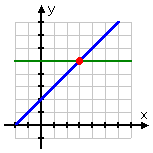
The intersection point is at x = 3, which was the solution value I'd found earlier. Similarly, when I was solving the equation , you could view this as me trying to find the intersection of the following two curves:

These two functions graph as:

Just as before, the solution is at x = 16.

But when I was trying to solve the nonsense equation , I was trying to find the intersection of the graph of the radical function and the constant function y₂ = −3, which do not intersect:

So what happened when I squared both sides of that nonsense equation? In a sense, I kind of "squared" both line equations, and got two new lines:

And, as the graph shows, these two new lines actually do intersect!

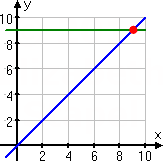
As you can see, squaring both sides of the original equation created a solution where none belonged. And the after-squaring solution did not work in the before-squaring equation, because the original lines had not intersected. This illustrates why I had to check my solution to figure out that the real answer was "no solution".

Warning: Many instructors do not to show many examples (in class or in the homework) of radical equations for which the solutions don't actually work. But then they'll put one or more of these on the next test. You should expect a "no solution" radical equation on the test, so you remember to check your solutions.