Solving Harder Radical Equations
Purplemath
Moving on from the simplest radical equations, we encounter equations in which the radical is not isolated. Sometimes, all we'll need to do is move a constant; other times, the solution will get rather messy.
-
Solve:
I could square both sides of the equation right away, but the radical isn't isolated on the left-hand side (because there's a 2 subtracted from it), so the result of squaring both sides at this stage won't be very helpful.
Here's what I get if I try squaring now:
Content Continues Below
Advertisement
I think I've made things worse! Rather than getting rid of the radical, I now have a radical term, plus a variable term outside of any radical. What now?
While squaring both sides at this point was not "wrong", it arguably wasn't much "right". (To complete the solution, I'd need to isolate the radical term, and then square both sides again.)
Instead of squaring right away, it will be more useful first to move the constant term 2 from the left-hand side of the equation over to the right-hand side. In this way, the radical will be isolated on the left:
I've isolated the square root, so now squaring both sides will work better:
Checking my solution, I find:
RHS: 5
LHS = RHS
The solution checks, so my answer is:
x = 49
Some radical equations can be simplified by first isolating the radical. But sometimes that won't be possible.
-
Find the solution:
This equation is a bit more messy than what we've seen before. I cannot isolate the radical because there are actually two radical terms. So how can I solve this algebraically? I'll have to square both sides twice. Here's what that looks like:
At this point, having finishing squaring once, I have managed to get the radical isolated on the right-hand side of the equation. Now I'll square for the second time:
Checking my solution, I get:
RHS: 3
LHS ≠ RHS
Hmm... All that work, and the only solution doesn't work in the original equation? Can that be right? I'll check the graph of the two lines corresponding to the two sides of the original equation to see if there appears to be an intersection point:
![y_1 = sqrt[x − 3] − sqrt[x] is a blue arc in the fourth quadrant; y_2 = 3 is a horizontal green line; no intersections are apparent in the graph](radicals/solve36.gif)
According to the graph, no, it does not appear that these lines ever intersect (and calculus techniques can prove this). So my answer is:
no solution
Content Continues Below
Why did it appear that there was a solution to that equation? Let's look at the graphs after the second squaring of the radicals (starred above, and repeated below):
y1 = x2 − 12x + 36
y2 = x2 − 3x
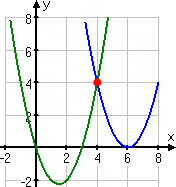
By squaring (twice, in this case), I had accidentally created a solution that hadn't existed for the original equation. Because I checked that solution in the original equation, I was able to see that the actual answer was that the equation had no solution.
Affiliate
Affiliate
Because these exercises are so lengthy to solve, your book or instructor may not provide many examples. Try not to be misled by the small sample sizes. Yes, the above equation with two radicals had no solution. But, no, this will not always be the case for equations with two radicals.
-
Find the solution:
This is the same as the previous equation, except that the sign between the radicals has been reversed. If I turn the left-hand and right-hand sides of this equation into their own functions, I get:
Graphing them, I get:
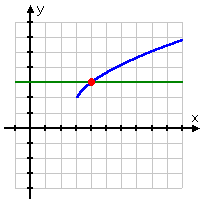
So this equation does have a solution, which appears to be around x = 4. To know the answer for sure, I have to do the algebra:
...and here's the check of my solution:
LHS = RHS
Since the solution works in the original equation, then the solution is valid, and the answer is:
x = 4
URL: https://www.purplemath.com/modules/solverad3.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()