Examples Using the Pythagorean Theorem
Purplemath
The Pythagorean Theorem arguably grew out of practical concerns of property lines, construction, digital music, GPS, and related geometric and physical concerns.
As a result, you should expect to encounter quite a few word problems that require the Theorem's use.
Content Continues Below
- Given the points (−2, −3), (2, 1), and (5, −2), determine if they are the vertices of a right triangle.
"Vertices" is the fancy name for corners, so this is asking me to figure out if the three points are the three corners of a right triangle. From a quick graph, I can see that the points are the corners of some sort of triangle:
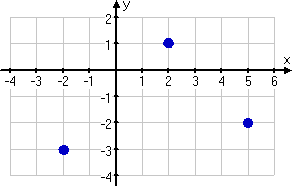
I can use the Distance Formula to find the lengths of the each of the sides of the triangle, these lengths being the distances between the pairs of points. Then I can plug these lengths into the Theorem to see if this triangle is a right triangle.
I think the points (−2, −3) and (5, −2) mark off the hypotenuse, assuming this triangle turns out to be right. (Note: The hypotenuse will always be the longest side so, when testing the sides in the Pythagorean Theorem, I will need to remember to plug the longest length into the variable c.)
(−2, −3) and (2, 1):
(2, 1) and (5, −2):
(−2, −3) and (5, −2):
Affiliate
Advertisement
Now I need to see if these lengths work in the Pythagorean Theorem. Of course, to use the Theorem, I'll need to use the squares of the three lengths, remembering that, if this does happen to be a right triangle, then the longest of the three sides is going to be the hypotenuse. So, when I plug into the Theorem, I'll need to use the largest value as the value of c.
To confirm (or disprove) that these three sides form a right triangle, I need to confirm (or disprove) that the sum of the squares of the lenggths of the two shorter sides is equal to the square of the length of the longest side. In other words, I need to add a2 and b2, and see if their sum matches c2.
a2 + b2 = 32 + 18 = 50
So the sum of the squares of the two smaller lengths equals the square of the largest length, proving that the three points they gave me are in fact the vertices of a right triangle.
These points are the vertices of a right triangle.
By the way, I could have saved myself a little time by working only with the squares. It's not like the exercise asked me for the lengths of the three sides and, to use the Theorem, I needed only the squares of those lengths. So I could have worked with the square d2 of each of the sides' lengths, avoiding square roots entirely.
Content Continues Below
- Zedekiah is building a gate. It is to be five feet tall and eight feet wide. If the gate is square (that is, if the gate has sides that meet at the corners to form right angles), what will be the length of the diagonal bracing wire? Round to the nearest quarter-inch.
I will assume that the gate is square. (Note: Something being square is different from the thing being *a* square. Being square just means that the corners form right angles, so a rectangle whose length is greater than its height is square, but it is not *a* square.)
The width of the gate (going horizontally), the height (going vertically), and the wire (going diagonally across) form a triangle. When the gate is square, that triangle will be a right triangle, the diagonal wire will be the hypotenuse of that triangle, and the triangle's sides' lengths will obey the Pythagorean Theorem.
I will square each of the two legs, being the width w and the height h. (The third side is the wire diagonal d.)
w2 = 82 = 64
h2 = 52 = 25
Now I'll plug these into the Pythagorean Theorem, and solve for the length d of the wire diagonal:
52 + 82 = c2
25 + 64 = 89 = c2
So the bracing wire will be nine feet long, plus another 0.43389 feet or so. There are twelve inches in one foot, so:
0.43389 × 12 = 5.20776
So there will be another about 5.2 inches, on top of the nine feet. They told me to round to the nearest quarter inch, and 0.2 is closer to 0.25 than it is to 0.0, so the length of the wire will be:
9 feet, 5 ¼ inches
Affiliate
This is not a real-world answer, of course. The wire will need to be attached to the gate somehow, such as by being wrapped around a bolt or other part of the gate's structure, and extra length will be required for that.
So the length they had me find is really the length of the wire from attachment-point to attachment-point. You'd need more than nine feet and five and a quarter inches of wire to actually brace the gate.
-
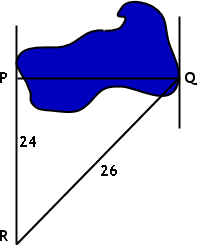
Zedekiah needs to find the width of the pond on a plot of land he's selling.
He has made measurements to point R from points P and Q on either side of the pond, and is certain that the angle at P is a right angle. (Labelled lengths are in meters.)
Assuming his measurements are correct, what is the width of the pond?
I have two sides of what is to be assumed to be a right triangle, so I can apply the Pythagorean Theorem to find the length of the third side. Since the angle at P is the (assumed) right angle, then QR is the hypotenuse, and:
262 = 242 + |PQ|2
676 = 576 + |PQ|2
100 = |PQ|2
10 = |PQ|
Looking back at the exercise, I see that the units for these measurements were meters; I need to include that unit in my answer.
The pond is ten meters across.
Note that, for the above answer to be correct, the displayed picture can not possibly be "to scale".
You should assume, as a matter of course, that the pictures for geometry and trigonometry exercises are not drawn to scale. Do not make the mistake of trying to guess the answers from the pretty pictures.
URL: https://www.purplemath.com/modules/pythagthm2.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()




