The Distance Formula
Purplemath
The Distance Formula is a variant of the Pythagorean Theorem that you used back in geometry. The Pythagorean Theorem allows you to relate the three sides of a right triangle; in particular, it allows you to find the length of the third side of a right triangle, given the lengths of the other two sides. The Distance Formula takes two points and implicitly assigns them the role of the hypotenuse.
Content Continues Below
Here's how we get from the one to the other:
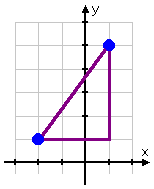
Suppose you're given the two points (−2, 1) and (1, 5), and they want you to find out how far apart they are. The points look like this:

You can draw in the lines, parallel to the two coordinate axes, that form a right-angled triangle, using these points as two of the corners:
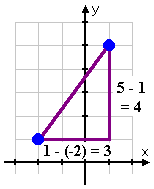
It's easy to find the lengths of the horizontal and vertical sides of the right triangle: just subtract the x-values and the y-values:
Then use the Pythagorean Theorem to find the length of the third side (which is the hypotenuse of the right triangle):
c2 = a2 + b2
...so:
c2 = (5 − 1)2 + (1 − (−2)2
Affiliate
This format always holds true. Given two points, you can always plot them, create the right triangle, and then find the length of the hypotenuse. The length of the hypotenuse is the distance between the two points. And since this format always works, it can be turned into a formula:
The Distance Formula: Given the two points (x1, y1) and (x2, y2), the distance d between these points is given by the formula:
Don't let the subscripts scare you, by the way. They only indicate that there is a "first" point and a "second" point; that is, that you have two points. Whichever one you call "first" or "second" is up to you. The distance between the two points will be the same, regardless of the order in which you used them.
Content Continues Below
Find the distance between the points (−2, −3) and (−4, 4).
To find my answer, I just plug the points' coordinates into the Distance Formula:
Then the distance is , or about 7.28, rounded to two decimal places.
URL: https://www.purplemath.com/modules/distform.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()