Introduction to Angles in Quadrants
Purplemath
You've worked with trigonometric ratios — sine, cosine, tangent, secant, cosecant, and cotangent — in a geometrical context; that is, in the context of right triangles.
Now we'll move those ratios into an algebraic context (being the Cartesian plane), and then we'll dispense with the triangles. This will allow us to work with angles greater than 90°.
Content Continues Below
Let's start with an equilateral triangle with sides of length 2:

Each angle of this triangle measures 60°.
Then let's drop the perpendicular, splitting the triangle into two 30-60-90 triangles:
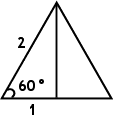
We'll work with that 60° angle, as labelled.
Now for the algebra:
We'll place the triangle on the x,y-plane, with the "adjacent" side on the x-axis, the "opposite" side parallel to the y-axis, and the angle we're working with, that 60° angle, at the origin:
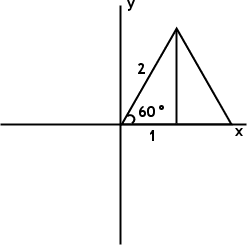
Now let's throw out the triangle, keeping just the base, the height, and the angle itself, along with the x- and y-values from the point on the terminal side of the angle which marks where the hypotenuse of the original 30-60-90 triangle had ended.
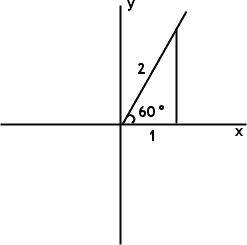
Since the length of the base is the same as the value of "adjacent", we can call this just "x". Similarly, the "opposite" is now just "y".
The Pythagorean Theorem gives us the value of the hypotenuse, which we will now call "r". Why? Because we can also look at this distance along the terminal side of the angle as being a radius line of a circle.
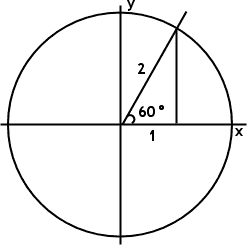
Any right triangle with the same-length hypotenuse will have its far vertex lying on this circle.
Affiliate
Advertisement
We already know that cos(60°) = ½. Now you can read this value from the drawing in the first quadrant. The cosine ratio, in the geometric context, had been "adjacent over hypotenuse"; now, in the algebraic context, it is "x over r". But the value is still ½.
So we've set up the angle in the first quadrant, thrown away the triangle, and still been able to find the trig ratio. Can we build on this? Yes!
Let's swing over to the second quadrant, drawing a similar line for 120°, being 60° above the negative x-axis. Since we're working in the same circle, we get the same value for r, but since we're in QII, we get a negative x-value: x = −1 instead of +1, as in the first quadrant:
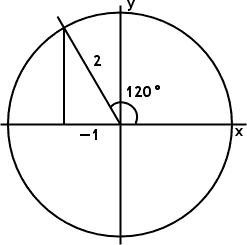
Now grab your calculator, make sure it's in "degree" mode, and plug in "cos(120°)". Did you get "−0.5"? That's the same as −½, right?
Now look again at the graph: x/r = (−1)/2 = −½ = −0.5, just like your calculator said!
Does this continue to work in the other quadrants? You bet!
Draw the corresponding line in QIII, marking 240°, being 60° below the negative x-axis. You can see from the picture that cos(240°) ought to be −½:
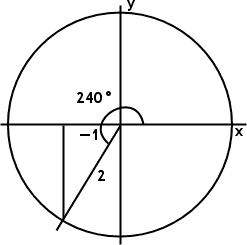
What does your calculator say?
Now let's move to QIV and draw the line for 300°, being 60° below the positive x-axis. In QIV, x is again positive, so cos(300°) = x/r = ½ = 0.5.
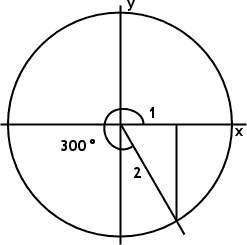
What does your calculator say?
Affiliate
Note that, in each case, all that really mattered was the sixty-degree triangle in the quadrant where the angle terminated, and the x- and y-values in that quadrant. The fact that you can't draw a right triangle with a base angle of 300° was completely irrelevant. To find the trig ratios, you needed only to draw the terminal side of the angle in whatever quadrant it happened to land, construct a right triangle by "dropping a perpendicular" (or, if below the axis, erecting the perpendicular) to the x-axis, and then work from there.
This works for all angles, and for all trigonometric ratios.
URL: https://www.purplemath.com/modules/quadangs.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()




