The Cartesian (or x, y-) Plane
Purplemath
Before the European Renaissance, math was cleanly divided into the two separate subjects of geometry and algebra. You didn't use algebraic equations in geometry, and you didn't draw any pictures in algebra.
(Which makes it amazing that Archimedes came very close to inventing calculus about 2,200 years ago. Can you imagine trying to do algebra using only geometric terms and concepts?
Content Continues Below
Advertisement
Affiliate
(For instance, what we express algebraically as x2 + 2x would, back in the day, have been expressed along the lines of "the area of a square with a certain side length, plus the lengths of two of those sides", or else it would have been written with symbolism that would make zero sense to us today. I mean, back then, they didn't even have the concept of equations. I have no idea how Archimedes accomplished what he did, but he must have been crazy smart.)
This state of affairs — algebra and geometry being completely separate areas of study — continued for ages. Then, around 1637, a French guy named René Descartes (pronounced "ray-NAY day-CART") came up with a way to put these two subjects together.
To explain Descartes' method, first think about using a paper map. Let's say you're trying to locate, within in a country you've never visited (say, Ukraine), a certain city (say, Chornobyl). To do so, you first look for the city's name in the map's index. Suppose the index says that your target city is located in D12. This tells you that you go across the top of the map and find the section whose width is labelled as "D", and then you go down the side and find the section whose height is labelled as "12".
![map of a portion of Ukraine, with letters A through I across the top, and numbers counting down, along the left-hand side, from 12 to 19. [The number 11, though not included, is implicitly the label for the top row that shows letters.]](xyplane/ukraine_map.png)
(Original public-domain image found at Machy.net)
Your fingers then trace down and across, with the section where they meet being the box labelled as "D12". Then you would look inside that box for the city you need (highlighted above).
Somebody figured out that this was a handy way to specify the right general area on the map, telling you how far over (the D) and how far up or down (the 12) you needed to go. Descartes originated the concept, and did something similar for mathematics.
Content Continues Below
You learned about the basic (counting) number line back in elementary school:
Later on, you were introduced to zero and negatives, which completed the number line:
What is the Cartesian plane?
The Cartesian ("karr-TEE-zhun") plane — named for its originator, René Descartes — is a way to precisely name points in the geometric plane. Descartes' breakthrough was in drawing the regular number line horizontally across the plane; then he took a second number line, rotated it to point upward, and crossed the first number line so they intersected at their zeroes:
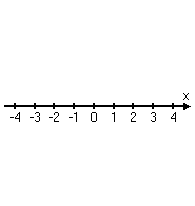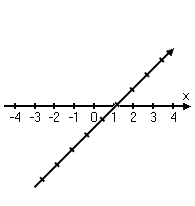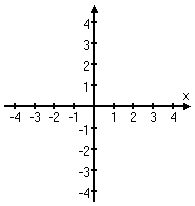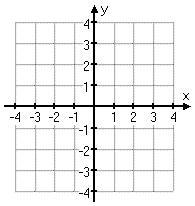
(The image above is an animation on the "live" page.)
The number lines, when drawn like this, are called "axes" (pronounced "ACK-seez"). The horizontal number line is called the "x-axis" ("eks-ACK-siss"); the vertical number line is the y-axis.
What is the origin?
The origin is where the two perpendicular number lines (that is, the two axes) cross. The number lines cross where each of x and y is zero, so the origin is located at the point (0, 0).
What do the axes' arrows mean?
The arrows at the ends of each of the axes indicate the direction in which the numbers are getting larger. Therefore, only the axes should have arrows, and the arrows should be on one end only.
Affiliate
Yes, many textbooks, especially in high school, draw the arrows incorrectly, as do many educators. (Don't point this out to them; for some reason, they're really touchy on this subject.) In real life, not all vertical axes point up and not all horizontal axes point to the right; in the sciences, the x-axis can point left; in finance, the y-axis often points down.
This information will be lost if you stick with the middle-school manner of splashing arrow-tips everywhere on every line.
The whole flat expanse, top to bottom, side to side, bursting outside of the box in the animation above and stretching off to infinity in all directions, is the plane. When you put the two axes in the plane, it is then the Cartesian plane.
How is "Cartesian" derived from "Descartes"?
The name "Cartesian" is derived from "Cartesius", which is the Latin version of "Descartes".
URL: https://www.purplemath.com/modules/plane.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()