Tricks to Make Solving Polynomials Less Painful
Purplemath
When you have a graphing calculator, you can whip out a quick graph of a given polynomial, and get a good idea from the picture of where the x-intercepts (that is, where the graphable zeroes) are. This is useful, because it can save you from wasting time trying out test zeroes that aren't reasonable.
Content Continues Below
So what do you do if you don't have a graphing calculator? Do you really have to try all the possible roots that the Rational Roots Test might spit out?
Not necessarily. There are a couple tricks you can use when working with synthetic division and the Rational Roots Test. The following is an example:
- Find all the roots of 2x3 + 7x2 − 16x + 6.
The Rational Roots Test gives the following list of possible zeroes:
For reference sake, here is the graph:
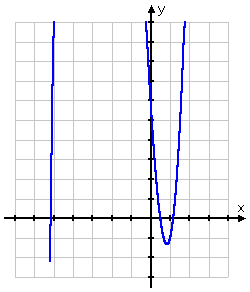
As you can see from the graph, the polynomial has no x-intercepts before (that is, to the left of) x = −6 and no x-intercepts after x = 2.
Affiliate
Working from the picture, I would guess that the zeroes are a little before x = −5, right at , and a little after x = 1.
I would guess that the rational zero will be at , and the other two zeroes will be irrational, generated by the square root in the Quadratic Formula.
But assuming I didn't have a graphing calculator handy, I won't have any of this information. So let's pretend we don't know what the graph looks like, and try x = −6 as our test zero:
Advertisement
The remainder is non-zero, so x = −6 is not a solution of the polynomial. But I notice something else when I look at the signs on the numbers in the bottom row. I divided by a negative, and the signs on the bottom row alternated (plus, minus, plus, minus).
The trick here is this: If, when using synthetic division, I divide by a negative and then I end up with alternating signs on the bottom row, then the test root was too low. (This does *not* work in reverse! You can sometimes divide by a too-low test root, but *not* get alternating signs on the bottom row!)
Now I'll try a test root that I know (from cheating and looking at the graph) is too high. I'll try x = 2 as the test zero:
The remainder is non-zero, so x = 2 is not a solution of the polynomial. But I notice something else when I look at the signed on the numbers in the bottom row. I divided by a positive, and the signs on the bottom row are all positive.
The trick here is this: If, when using synthetic division, I divide by a positive and end up with all positive numbers on the bottom row, then the test root was too high. (This does *not* work in reverse! You can sometimes divide by a too-high test root, but *not* get all positive numbers on the bottom row!)
Content Continues Below
Note: For either of these two tricks / rules, the number 0 may be counted as positive or negative (though technically it is neither), according to whichever pattern I'm trying to match. For instance, if I'd divided by a negative and my bottom row had been 1 −3 2 0 4 −5, then I would have counted the 0 as being negative and the signs would have been alternating, telling me that my test root was too low. In similar manner, if I'd divided by a positive and my bottom row had been 1 3 2 0 4 5, then I would have counted the 0 as being positive and all the signs would have been positive, telling me that my test root was too high.
Warning: These are the *only* two patterns. If you divide by a negative and get all positives, all negatives, or any pattern other than alternating signs, then the bottom row tells you nothing. You cannot conclude anything about whether or not the test root was too low (or too high). And if you divide by a positive and get all negatives, alternating signs, or any pattern other than all positives, then the bottom row tells you nothing. You cannot conclude anything about whether or not the test root was too high (or too low). In practice, this means that generally the bottom row won't tell you much!
Getting back to the problem at hand:
I now know that x = −6 is too low. Wherever my zeroes are, they're above x = −6. So now I'll try x = −2 (pretending for the moment that I don't know, from the graph, that this value is not a root):
The bottom row does not have alternating signs, so I can't tell from this whether or not x = −2 is too low. (From the picture, I know that this test point is actually between two zeroes. But I cannot tell this from the synthetic division.)
However, I can conclude something useful from this result.
Affiliate
Since the remainder for the first division was −78, this meant that f(−6) = −78, by the Remainder Theorem. The division that I just did says that f(−2) = 50.
Since f(−6) is negative (that is, this point on the graph is below the x-axis) and f(−2) is positive (that is, this point on the graph is above the x-axis), then the graph must cross the x-axis somewhere between x = −6 and x = −2.
In other words, the results of these two divisions tell me that there must be a zero of the polynomial between x = −6 and x = −2. The only candidate (from the list that the Rational Roots Test gave me) is x = −3, so I'll try that:
Nope; whatever is the value of the zero, the zero between x = −6 and x = −2, it isn't rational. However, since f(−3) = 63, which is positive, then I have narrowed down the location of the irrational zero: it will be between x = −6 and x = −3.
I still need to find a zero, so now I'll try x = 1, since I know that x = 2 is too high:
While the bottom row is not all positive (so I cannot conclude that x = 1 is too high), I can conclude that a zero must lie between x = 1 and x = 2, because f(1) = −1 is negative, and f(2) = 18 is positive. The only rational candidate is , so I'll try that:
Nope; isn't a zero either. So the zero between x = 1 and x = 2 must be the other irrational root from the Quadratic Formula, the pair to the irrational root between x = −6 and x = −3. The rational root must lie elsewhere.
Since f(−2) = 48 is positive and f(1) = −6 is negative, there must be a zero between x = −2 and x = 1. The available rational test points are , x = −1, , and . One of these values must be the rational zero.
Another trick I can use comes from Descartes' Rule of Signs, which says that there is one negative root and either two or zero positive roots. Since I have already figured out that there is an irrational root between x = −6 and x = −3 (so the negative root has already been partially located), then any rational root must be positive. Therefore, I can cross , x = −1, and off my list of possible roots.
The only remaining rational possibility is , so I'll try that:
Aha! I've finally found my rational root! And dividing out (that is, dividing out the factor ) leaves me with a quadratic which I can solve, starting by dividing through by 2:
2x2 + 8x − 12 = 0
x2 + 4x − 6 = 0
(I don't actually need the approximate values of the two irrational zeroes, because I'm not graphing the cubic polynomial. I will hand in only the exact values, with the square roots.)
Then the zeroes are:
These polynomial-solution problems are usually long and annoying like this. You can probably see how looking at a graph can be very useful! But if you don't have access to a graphing calculator, you can (eventually) get the correct answer. I would recommend that you practice, so you can get a feel for how these work. That way, you can quickly process these questions, and not waste too much time on your tests.
On the next page, I'll show you how this works when I have *not* cheated and peeked at the graph first.
URL: https://www.purplemath.com/modules/synthtrk.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()




