Conjugates / Dividing by Square Roots

The Purplemath Forums
Helping students gain understanding
and self-confidence in algebra

Return to the Lessons Index | Do the Lessons in Order | Get "Purplemath on CD" for offline use | Print-friendly page

Conjugates / Dividing by Square Roots (page 4 of 7)

Sections: Square roots, More simplification / Multiplication, Adding (and subtracting) square roots, Conjugates / Dividing by square roots, Rationalizing denominators, Higher-Index Roots, A special case of rationalizing / Radicals & exponents / Radicals & domains

Simplify

I do the multiplication:

multiplication

Then I complete the calculations by simplifying:

(sqrt(3) + sqrt(5)) (sqrt(3) - sqrt(6)) = 3 + sqrt(15) - 3sqrt(2) - sqrt(30)

Simplify:

I do the multiplication:

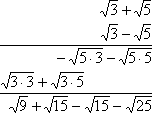
multiplication

Then I simplify:

(sqrt(3) + sqrt(5)) (sqrt(3) - sqrt(5)) = 3 - 5 = -2

Note in the last example above how I ended up with all whole numbers. (Okay, technically they're integers, but the point is that the terms do not include any radicals.) I multiplied two radical "binomials" together and got an answer that contained no radicals. You may also have noticed that the two "binomials" were the same except for the sign in the middle: one had a "plus" and the other had a "minus". This pair of factors, with the second factor differing only in the one sign in the middle, is very important; in fact, this "same except for the sign in the middle" second factor has its own name:

Given the radical expression , the "conjugate" is the expression .

The conjugate (KAHN-juh-ghitt) has the same numbers but the opposite sign in the middle. So not only is the conjugate of , but is the conjugate of .

When you multiply conjugates, you are doing something similar to what happens with a difference of squares:

	ADVERTISEMENT

When you multiply the factors a + b and a – b, the middle "ab" terms cancel out:

(a + b)(a - b) = a^2 + ab - ab - b^2 = a^2 - b^2

The same thing happens when you multiply conjugates:

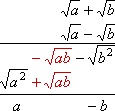
(sqrt(a) + sqrt(b)) (sqrt(a) - sqrt(b)) = a - b

We will see shortly why this matters. To get to that point, let's take a look at fractions containing radicals in their denominators.

Dividing by Square Roots

Just as you can swap between the multiplication of radicals and a radical containing a multiplication, so also you can swap between the division of roots and one root containing a division.