Print-friendly page

Multiplying and Dividing Negative Numbers (page 3 of 4)

Sections: Introduction, Adding and subtracting, Multiplying and dividing, Negatives and exponents

Turning from addition and subtraction, how do you do multiplication and division with negatives? Actually, we've already covered the hard part: you already know the "sign" rules:

plus times plus is plus  (adding many hot cubes raises the temperature)

minus times plus is minus  (removing many hot cubes reduces the temperature)

plus times minus is minus  (adding many cold cubes reduces the temperature)

minus times minus is plus  (removing many cold cubes raises the temperature)

The sign rules work the same way for division; just replace "times" with "divided by". Here are a couple examples of the rules in division:   Copyright © Elizabeth Stapel 2006-2008 All Rights Reserved

(Remember that fractions are just another form of division!)

You may notice people "canceling off" minus signs. They are taking advantage of the fact that "minus times minus is plus". For instance, suppose you have (–2)(–3)(–4). Any two negatives, when multiplied together, become one positive. So pick any two of the multiplied (or divided) negatives, and "cancel" their signs:

• Simplify (–2)(–3)(–4).

(–2)(–3)(–4)  
    = (–2)(–3)(–4)  
    = (+6)(–4)  
    = –24

So if you're given a long multiplication with negatives, just cancel off in pairs:

• Simplify (–1)(–2)(–1)(–3)(–4)(–2)(–1).

(–1)(–2)(–1)(–3)(–4)(–2)(–1)
    = (–1)(–2)(–1)(–3)(–4)(–2)(–1)
    = (+1)(+2)(–1)(–3)(–4)(–2)(–1)
    = (1)(2)(–1)(–3)(–4)(–2)(–1)
    = (1)(2)(+1)(+3)(–4)(–2)(–1)
    = (1)(2)(1)(3)(–4)(–2)(–1)
    = (1)(2)(1)(3)(+4)(+2)(–1)
    = (1)(2)(1)(3)(4)(2)(–1)
    = (2)(3)(4)(2)(–1)
    = 48(–1)
    = –48

Here's another example:

Negatives through parentheses

The major difficulty that people have with negatives is in dealing with parentheses; particularly, in taking a negative through parentheses. The usual situation is something like this:

–3(x + 4)

If you had "3(x + 4)", you would know to "distribute" the 3 "over" the parentheses:

3(x + 4) = 3(x) + 3(4) = 3x + 12

The same rules apply when you're dealing with negatives. If you have trouble keeping track, use little arrows:

Here are a couple more examples:

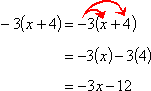
• Simplify 3(x – 5).

3(x – 5) = 3(x) + 3(–5) = 3x – 15

• Simplify –2(x – 3).

–2(x – 3) = –2(x) – 2(–3) = –2x + 2(+3) = –2x + 6

The other trouble, related to the previous one, is with subtracting a parentheses. You can keep track of the subtraction sign by converting the subtraction to a multiplication by negative one:

• Simplify 4 – (2 + x).

Don't be afraid to write in the little "1" and draw in the little arrows. You should do whatever you need to do to keep your work straight and get the right answer. Here are more examples:

• Simplify 6 – (3x – 4[1 – x]).

• Simplify ¹/₃  –   ^{(x – 2)}/₃.

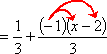
Note that I converted from subtracting a fraction to adding a negative one times a fraction. It is very easy to "lose" the minus when you're adding messy polynomial fractions like this. The most common mistake is to put the minus on the x and forget to take it through to the –2. Take particular care with fractions!

<< Previous  Top  |  1 | 2 | 3 | 4  |  Return to Index  Next >>

  Copyright © 2006-2008  Elizabeth Stapel   |   About   |   Terms of Use

 Feedback   |   Error?