The Order of Operations: PEMDAS
Purplemath
If you are asked to simplify something like "4 + 2×3", the question that naturally arises is "Which way do I do this? Because there are two options!" I could add first:
4 + 2×3 = (4 + 2)×3 = 6×3 = 18
...or I could multiply first:
4 + 2×3 = 4 + (2×3) = 4 + 6 = 10
Which answer is the right one?
Content Continues Below
It seems as though the answer depends on which way you look at the problem. But we can't have this kind of flexibility in mathematics; math won't work if you can't be sure of the answer, or if the exact same expression can be calculated so that you can arrive at two or more different answers. Mathematics doesn't do "loosey-goosey".
Affiliate
Advertisement
To fix this "it depends on how you look at it" issue, mathematicians codified an ordering to the arithmetical operations of addition, subtraction, multiplication, division, repeated multiplication (that is, exponentiation), and grouping (that is, parentheticals). This codification of which comes before what is called "the order of operations".
What is the order of operations?
The order of operations is a listing of the basic mathematical operations according to precedence (that is, according to which operation is applied first, then which is applied second, etc). The ordering says that anything inside a parenthetical is simplified first; then exponents are applied; then multiplication and division are applied (going from left to right), and finally addition and subtraction are applied (again, going from left to right).
The order of operations was established informally at least as far back as the 1500s; by "informally", I mean that mathematicians just sort of agreed that the ordering made sense. The order of operations does not seem to have been formalized until the early 1900s. (For more on the history of the formalization of the order of operations, try TheMathDoctors.)
How can I remember the order of operations?
A common technique for remembering the order of operations is the abbreviation (or, more properly, the acronym) "PEMDAS", which has been turned into the mnemonic phrase "Please Excuse My Dear Aunt Sally". This phrase stands for, and helps one remember the order of:
- Parentheses,
- Exponents,
- Multiplication and Division, and
- Addition and Subtraction
This listing tells you the ranks of the operations: Parentheses outrank exponents, which outrank multiplication and division (but multiplication and division are at the same rank), and multiplication and division outrank addition and subtraction (which are together on the bottom rank). In other words, the precedence is:
- Parentheses (simplify inside 'em)
- Exponents (apply them)
- Multiplication and Division (going from left to right)
- Addition and Subtraction (going from left to right)
When you have a bunch of operations of the same rank, you just operate from left to right. For instance:
15 ÷ 3 × 4
...is not 15 ÷ (3 × 4) = 15 ÷ 12, but is actually:
(15 ÷ 3) × 4 = 5 × 4 = 20
...because, going from left to right, you get to the division sign first.
If you're not sure of this, test it in your calculator, which has been programmed with the Order-of-Operations hierarchy. For instance, typesetting the above expression into a graphing calculator, you will get:

Using the above hierarchy, we see that, in the "4 + 2 × 3" question at the beginning of this article, Choice 2 was the correct answer, because we have to do the multiplication before we do the addition.
Content Continues Below
What is BODMAS? or BEDMAS? or BIMDAS
Speakers of British English often instead use the acronym "BODMAS", rather than "PEMDAS". BODMAS stands for "Brackets, Orders, Division and Multiplication, and Addition and Subtraction". Since "brackets" are grouping symbols like parentheses, and since "orders" is another word for exponents, the two acronyms mean the same thing. (The I in BIMDAS stands for "indices", which is another word for exponents.) Also, note that the "M" and the "D" are reversed in the British-English version; this confirms that multiplication and division are at the same "rank" or "level".
Canadian English-speakers split the difference, using BEDMAS.
Why does "order" mean "exponent"?
In case you're wondering why British-English uses the word "orders" to stand for "exponents", it appears that nobody knows. The Wikipedia source for this equivalence is — I'm not making this up — the page you're reading right now. I can find no formal etymology for this usage. The canonical source for math-word origins only mentions order in the sense of the degree; its closest approach to orders as exponents is "parodick degrees", which refers to a polynomial having its terms in decreasing order. So your guess as to "why 'orders'?"is probably as good as anybody else's.
The order of operations was settled upon in order to prevent miscommunication, but PEMDAS can generate its own confusion. Many students using PEMDAS think that multiplication *must* be done before division; students using BODMAS think that addition *must* be done before subtraction. But multiplication and divison are on the same level, because division is just multiplication by the reciprocal; and addition and subtaction are on the same level, because subtraction is just addition of a negative. (The acronym could maybe be restated as BOPS, meaning "brackets, orders, products, and sums".)
Probably the best way to explain this is to work through some examples:
- Simplify 4 + 32.
I need to simplify the term with the exponent before trying to add it to the 4:
4 + 32
= 4 + 9
= 13
- Simplify 4 + (2 + 1)2.
I have to simplify inside the parentheses before I can take the exponent through. Only then can I deal with the addition of the 4.
4 + (2 + 1)2
= 4 + (3)2
= 4 + 9
= 13
- Simplify 4 + [−1(−2 − 1)]2.
Affiliate
I shouldn't try to do these nested parentheses from left to right; attempting to simplify that way is way too error-prone. Instead, I'll try to work from the inside out.
First I'll simplify inside the curvy parentheses, then I'll simplify inside the square brackets, and only then will I take care of the squaring. After that is done, then I can finally add in the 4:
4 + [−1(−2 − 1)]2
= 4 + [−1(−3)]2
= 4 + [3]2
= 4 + 9
= 13
How do I know what grouping symbols to use?
There is no particular significance in the use of square brackets (the "[" and "]" above) instead of parentheses. Brackets and curly-braces (the "{" and "}" characters) are often used when there are nested parentheses, as an aid to keeping track of which close-parentheses go with which open-parens. The different grouping characters are used for convenience only.
This is similar to what happens in a spreadsheet when you enter a formula using parentheses: each set of parentheses is color-coded, so you can tell the pairs:
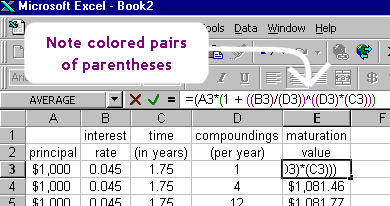
- Simplify
I will simplify inside the parentheses first, and only then multiply by the 4. Yes, this means that I'll be adding before doing the multiplication, but that's okay; the addition is inside grouping symbols, so it comes first.
So my simplified answer is
URL: https://www.purplemath.com/modules/orderops.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()




