Return to the Purplemath home page

 

Return to the Lessons Index  | Do the Lessons in Order  |  Print-friendly page

Exponential Functions: Evaluation (page 2 of 5)

Sections: Introduction, Evaluation, Graphing, Compound interest, The natural exponential

The first thing you will probably do with exponential functions is evaluate them.

  • Evaluate 3x at x = –2, –1, 0, 1, and 2.

    To find the answer, I need to plug in the given values for x, and simplify:

      T-chart for y = 3^x

  • Given f(x) = 3–x, evaluate f(–2), f(–1), f(0), f(1), and f(2).

    To find the answer, I need to plug in the given values for x, and simplify:

      T-chart for f(x) = 3^(-x)

Take another look at the values I came up with: they were precisely reversed between the two T-charts. Remember that negative exponents mean that you have to flip the base to the other side of the fraction line. This means that 3–x may also be written as ( 1/3 )x, by taking the "minus" in the exponent and using it to flip the base "3". With this in mind, you should be able to predict the values for the following problem:   Copyright © Elizabeth Stapel 2002-2011 All Rights Reserved

  • Given g(x) = ( 1/3 )x, evaluate for x = –2, –1, 0, 1, and 2.

Advertisement

    Plug in the given values for x, and simplify:

      T-chart for g(x) = (1/3)^-x

This exercise points out two things. First, you really do need to be good with exponents in order to do exponentials (so review the topic, if necessary), and, second, exponential decay (getting smaller and smaller by half (or a third, or...) at each step) is just like exponential growth, except that either the exponent is "negative" (the "–x" in "3–x") or else the base is between 0 and 1 (the "1/3" in "( 1/3 )x").

It will likely be necessary for you to be able to just look at an equation or an expression or a graph and correctly identify which type of change it represents, growth or decay, so go back and study the above examples, if you're not sure of what is going on here.

 
To be thorough, since 3x models growth:

  

 graph of 3^x

  

 
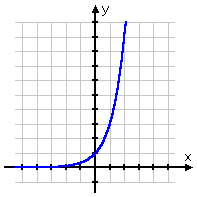
...and since 3–x and ( 1/3 )x model decay:

  

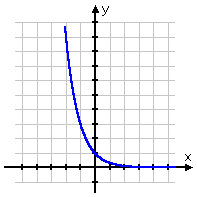
 graph of 3^(-x) and also of (1/3)^x

...it seems reasonable that ( 1/3 )–x (small base and a "negative" exponent) should model growth. Let's check....

<< Previous  Top  |  1 | 2 | 3 | 4 | 5  |  Return to Index  Next >>

Cite this article as:

Stapel, Elizabeth. "Exponential Functions: Evaluation." Purplemath. Available from
    https://www.purplemath.com/modules/expofcns2.htm. Accessed
 

 

Purplemath:
  Linking to this site
  Printing pages
  School licensing

Reviews of
Internet Sites:
   Free Help
   Practice
   Et Cetera

The "Homework
   Guidelines"

Study Skills Survey

Tutoring from Purplemath
Find a local math tutor

  Copyright © 2002-2012  Elizabeth Stapel   |   About   |   Terms of Use

 

Contact Us