Exponential Functions: The "Natural" Exponential e
Purplemath
There is one very important number that arises in the development of exponential functions, and that is the "natural" exponential.
(If you really want to know about this number, you can read the book "e: The Story of a Number", by Eli Maor.)
Content Continues Below
In the formula for compound interest, recall that n stands for the number of compoundings in a year. What happens when you start compounding more and more frequently? What happens when you go from yearly to monthly to weekly to daily to hourly to minute-ly to second-ly to...?
What happens if you compound faster and faster?
Ignoring the principal, the interest rate, and the number of years by setting all these variables equal to "1", and looking only at the influence of the number of compoundings n, we get the following values:
| how often compounded |
computed value |
|---|---|
| yearly | |
| semi- annually |
|
| quarterly | |
| monthly | |
| weekly | |
| daily | |
| hourly | |
| every minute |
|
| every second |
As you can see, the computed value keeps getting larger and larger, the more quickly you compound. But the growth is slowing down as n gets bigger; as the number of compoundings per year increases, the computed value appears to be approaching some fixed value. You might think that the value of the compound-interest formula is getting closer and closer to a number that starts out 2.71828, and you'd be right; the number we're approaching is called e, the "natural" exponential.
Affiliate
Advertisement
If you think back to geometry, you'll remember the number π, which was approximated by the decimal 3.14159 or by the fraction . Remember that we call π by the name "π" and use a symbol for this number because π never ends when written as a decimal. It's not a nice, neat number like 2 or ; π is instead an irrational number.
But it's an important number; you'd have real trouble doing geometry without it. So we gave this useful number the name "π", to simplify our calculations and communication, because it's a lot easier to say "π" than to say "3.141592653589 and so on forever" every time we need to refer to this number. We gave the number a letter-name because that was easier.
In the same way, this compound-interest number is also very useful. You may not see the usefulness of it yet, but it is vital in physics and other sciences, and you can't do calculus without it. As with π, listing out its first dozen or so digits every time we refer to this number gets to be annoying, so we call it by the name "e".
The number e is the "natural" exponential because it arises naturally in math and the physical sciences (that is, it arises naturally in real life situations), just as π arises naturally in geometry. This number was named, in the 1720's or 1730's, by a guy named Leonhard Euler (his last name is pronounced "OY-lerr"), who swore that this name stood for "exponential", and not for his own last name.
(The number is sometimes called "Napier's constant", because John Napier implicitly used it in 1618 when he prepared some logarithm tables. The number was actually explictly derived and pointed out by Jacob Bernoulli; he found the number in 1683 by working with the compound-interest formula.)
Your calculator can do computations with e; it is probably a second function on your calculator, right above the "ln" or "LN" key on your calculator. If you're not sure where this is on your calculator, go check now, and get used to the syntax (that is, the correct keys to use, in the correct order) that your particular model uses. You're gonna need it.
Content Continues Below
What is an example of evaluating with e?
- Given f (x) = ex, evaluate f (3), rounding to two decimal places.
I need to plug this into my calculator. (Check your owner's manual, if you're not sure of the key sequence.) I get:
f (3) = 20.0855369232...
Rounded to two decimal places, my answer is:
f (3) = 20.09
What is an example of graphing a function with e?
- Graph y = e2x.
Since the base e is greater than 1, and since the power 2x is positive (in the sense of there being no "minus" sign on the exponent), then the graph should look like exponential growth.
First, I will compute some plot points:
Then I'll draw the graph:
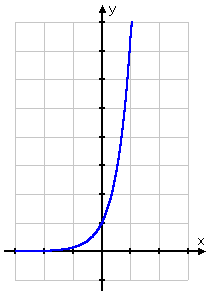
Make sure, when you are evaluating e2x, that you format the expression correctly. Either multiply out the 2x first, and then apply it to the e, or else put the 2x inside parentheses. Otherwise, the calculator will think you mean e2 × x, and will return the wrong values, as you can see below:

Every once in a while they'll give you a more-complicated exponential function to deal with:
- Graph y = ex2.
I will compute some plot-points, as usual:
For graphing, the decimal approximations are more useful than the "exact" forms. For instance, it is hard to know where e2.25 should be plotted, but it's easy to find where 9.488 goes (namely, right around 9.5 units above the x-axis). So I'll use the "exact" value for my hand-in T-chart, but I'll use the decimal approximations for drawing my graph.
Note also that I calculated more than just whole-number points. The exponential function grows way too fast for me to use a wide range of x-values (I mean, look how big y got when x was only 2). Instead, I had to pick some in-between points in order to have enough reasonable dots for my graph.
Now I plot the points, and draw my graph:
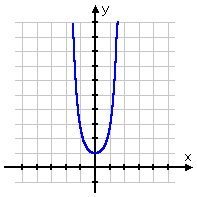
The above graph doesn't look like the typical exponential shape. This is because the exponent is not a simple linear expression. You should expect to see one or two of these graphs on the next test. In practical terms, though, the typical shape is what you'll usually be seeing and using.
Affiliate
Your teacher or book may go on at length about using other bases for growth and decay equations, but, in real life (such as physics), the natural base e is generally used.
The equation for "continual" growth (or decay) is A = Pert, where A is the ending amount, P is the beginning amount (for example, principal, in the case of money), r is the growth or decay rate (where the percent is always expressed as a decimal), and t is the time (in whatever unit was used on the growth/decay rate).
Make sure you have memorized this equation, along with the meanings of all the variables. You are almost certain to see it again, especially if you are taking any classes in the sciences.
(This equation helped me pass a chemistry class. I really didn't know what the teacher was talking about, but all the test problems worked off this equation, so I just plugged in all the given information, and solved for whichever variable was left. I'm not saying this to advocate being clueless in chemistry, but to demonstrate that the continuously-compounded formula really is a useful equation.)
The continuous-growth formula is first given in the above form A = Pert, using r for the growth rate, but will later probably be given as A = Pekt, where k replaces &r, and stands for "growth (or decay) constant".
Or different variables may be used, such as Q = Nekt, where N stands for the beginning amount and Q stands for the ending amount.
The point is that, regardless of the partiular letters being used, the formula itself remains the same. And you should be familiar enough with the formula to recognize it, no matter what letters they happen to have plugged into it.
What is an example of a continuous-growth exercise?
- Certain bacteria, given favorable growth conditions, grow continuously at a rate of 4.6% a day. Find the bacterial population after thirty-six hours, if the initial population was 250 bacteria.
As soon as I read "continuously", I should be thinking "continuously-compounded growth formula". "Continuously" is the buzz-word that tells me to use A = Pert.
The beginning amount was P = 250; the growth rate is r = 0.046. I'll to convert the thirty-six hours into days; this tells me that the time t for this exercise is days.
(Why is "time" converted to days this time, instead of to years? Because the growth rate was expressed in terms of a given percentage per day. The rates in the compound-interest formula for money are always annual rates, which is why t was always in years in that context. But this is not the case for the general continual-growth/decay formula; the growth/decay rates in other, non-monetary, contexts might be measured in minutes, hours, days, etc. And I always need to remember to check the time period given, so that I can be sure to make everything match.)
I plug in the known values, and simplify for the answer:
A = 250e(0.046)(1.5)
= 250e(0.069)
= 267.859052287...
There will be about 268 bacteria after thirty-six hours.
By the way, if you do your calculations "inside-out", instead of left-to-right, you will be able to keep everything inside the calculator, and thereby avoid round-off error.
For example, the computation above (that gave the number of bacteria), done inside-out, would look like this:

URL: https://www.purplemath.com/modules/expofcns5.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()