Intro to Adding (and Subtracting) Rational Expressions
Purplemath
Addition and subtraction are the hardest things you'll be doing with rational expressions because, just like with regular fractions, you'll have to convert these polynomial fractions to their lowest common denominators. Everything you hated about adding fractions, you're gonna to hate worse with rational expressions. But stick with me; you *can* do this!
Content Continues Below
Let's refresh by looking at an example with regular (that is, strictly numerical) fractions:
- Simplify the following:
To find the common denominator, I first need to find the least common multiple (LCM) of the three denominators. (For old folks like me, whenever you see "LCM", think "LCD", or "lowest common denominator". In this context, they're pretty much the same thing.) There are at least a couple ways of doing this. I could use the "listing" method, where I list the multiples of the three denominators until I find a number that is in all three lists, like this:
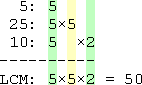
5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55,...
25: 25, 50, 75, 100, 125, 150, 175, 200,...
10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100,...
The first multiple to occur in all three lists is 50, so this will be the lowest common denominator.
Another method I could use (and this is the method I prefer) for finding the common denominator is the factor method. It works by finding the prime factorization of each denominator, and then using a chart to find the factors needed for the common denominator. It looks like this:
Affiliate
Advertisement
In either case, the common denominator will be 50.
To convert each fraction to the common denominator, I will multiply each denominator by what it needs in order to turn it into 50. For instance, in the , the denominator needs to be multiplied by 10, since 10 × 5 = 50. To keep things fair, I multiply the top by 10 as well. This is because 10 ÷ 10 = 1, and multiplying things by 1 doesn't actually change them. So I get:
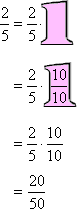
Converting the other fractions to the same denominator, I get:
This doesn't simplify or reduce, so my final answer is:
Content Continues Below
The process works similarly for rational expressions.
How do you add rational expressions?
- Find the lowest common denominator for the assorted polynomial fractions.
- Convert each of the rational expressions to this common denominator.
- Add the numerators.
- Simplify, if possible. (It usually won't be.)
What does this look like, in practice? Let's dive in:
- Simplify the following:
To find the common denominator, I need to find the least common multiple of x, x2, and 2x.
Affiliate
In the strictly-numerical example above, I used the "listing" method to find the common denominator: all I had to do was multiply each denominator by 1, then 2, then 3, then 4,... and so on, until I found a match.
But in this case, I've got numbers and variables, so just multiplying by numbers is not going to work.
Clearly, the "listing" method won't work for rational expressions. I'll have to use the factor method instead. Here's what I get:
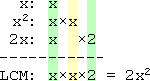
So my common denominator for these polynomial fractions will be 2x2. To convert the to the common denominator, I will need to multiply by . Why? Because the denominator already has one copy of x, but it needs a 2 and a second copy of x:
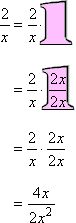
Similarly, for the , I will multiply by ; and for the , I will multiply by . This gives me:
Then the answer is:
This expression cannot be further simplified!
The x's cannot cancel off, and the 2 cannot cancel into the 6. Why not? Because you can only cancel factors, not terms. You cannot reach inside the understood parentheses around the "5x + 6" factor and rip off arms and legs in an effort to beat the denominator into submission. Don't even try!
URL: https://www.purplemath.com/modules/rtnladd.htm
You can use the Mathway widget below to practice adding rational expressions. Try the entered exercise, or type in your own exercise. Then click the button and select "Simplify" or "Add" to compare your answer to Mathway's.
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()