LCM and GCF
Purplemath
What is the LCM?
"LCM" stands for "least common multiple". Given two numbers, their LCM is the least (that is, the smallest) common (that is, shared) multiple of those two numbers. For instance, given the two numbers 4 and 5, their LCM is the smallest number that includes each of 4 and 5 as factors; in this example, the LCM is 20.
Content Continues Below
What is the GCF?
"GCF" stands for "greatest common factor". Given two numbers, the GCF is the greatest (that is the largest) common (that is, shared) factor of those two numbers. For instance, given the numbers 15 and 18, their GCF is the biggest number that is a factor of (that is, that divides cleanly into) each of 15 and 18; in this example, the GCF is 3.
How do you find the LCM?
There are two methods for finding the LCM of a pair of numbers. The first method requires that you make lists (very long lists, sometimes) of all the numbers that are multiples of the original numbers; you keep listing until you finally find a match, being some multiple that is common to both listings. The second method requires only the prime factorization of the two numbers, followed by (here's the trick!) making a nice neat grid.
How do you find the GCF?
Affiliate
There are two methods for finding the GCF of a pair of numbers. The first method requires that you make a complete list (a very long list, sometimes) of all the numbers that divide evenly into the original numbers; you then compare the two listings, hoping for a match. If there is a match, this number is a common factor; if there is only the one match, then this is the GCF of the two numbers. If there is more than one match, then you take the largest match as the GCF. If there is no match, then the number 1 is the GCF. (The number 1 is, trivially, a factor of every number.) The second method requires only the prime factorization of the two numbers, followed by (here's the trick again!) making a nice neat grid.
Here's an example that uses the first method:
- Find the GCF and LCM of 2940 and 3150.
To find the Greatest Common Factor, I need to find all of the factors, prime and otherwise, of each of the two numbers. The best way I've found to do this is to find factor pairs; that is, I'll find one number that divides evenly into the number, and then do the division, which gives me the other factor in the pair. So, grabbing my calculator...
2940: 1×2940, 2×1470, 3×980, 4×735, 5×588, 6×490, 7×420, 10×294, 12×245, 14×210, 15×196, 20×147, 21×140, 28×105, 30×98, 35×84, 42×70, 49×60
3150: 1×3150, 2×1575, 3×1050, 5×630, 6×525, 7×450, 9×350, 10×315, 14×225, 15×210, 18×175, 21×150, 25×126, 30×105, 35×90, 42×75, 45×70, 50×63
(I found these factor pairs by dividing the original numbers in my calculator by progressively larger values, starting at 2 and continuing until the answer after division was smaller than what I'd divided by.)
Now I list the factors in order, from least to greatest:
2940: 1, 2, 3, 4, 5, 6, 7, 10, 12, 14, 15, 20, 21, 28, 30, 35, 42, 49, 60, 70, 84, 89, 105, 140, 147, 196, 210, 245, 294, 420, 490, 588, 735, 980, 1470, 2940
3150: 1, 2, 3, 5, 6, 7, 9, 10, 14, 15, 18, 21, 25, 30, 35, 42, 45, 50, 63, 70, 75, 90, 105, 126, 150, 175, 210, 225, 315, 350, 450, 525, 630, 1050, 1575, 3150
The largest value that is in both lists is 210, so this is the GCF.
Now I have to start listing the multiples of each of the original numbers, until I find a duplicate:
2940: 2940, 5880, 8820, 11760, 14700, 17640, 20580, 23520, 26460, 29400, 32280, 38220, 41160, 44100, 47040, 49980,...
3150: 3150, 6300, 9450, 12600, 15750, 18900, 22050, 25200, 28350, 31500, 34650, 37800, 40950, 44100,...
While I was making my list of multiples of 3150, I had to keep extending my list of multiples of 2940, until I finally found a duplicate. This duplicate, 44100, is the LCM.
GCF: 210
LCM: 44100
Content Continues Below
Okay; that was the painful way of finding the LCM and GCF. Here's the other, much easier and faster, way:
- Find the GCF and LCM of 2940 and 3150.
First, I need to factor factor each of the numbers they've given me:
2)2940
-----
2)1470
-----
3)735
----
5)245
----
7)49
---
7
(This factorization process is pretty easy: divide by the smallest prime that goes in evenly, working your way through the primes until the answer to your division is itself a prime. Review this lesson if you need a refresher.)
Now I'll apply the same sequential-division process to 3150:
2)3150
-----
3)1575
-----
3)525
----
5)175
----
5)35
---
7
The factorizations can be read from the numbers along the outside of the sequential divisions, so my prime factorizations are:
2940 = 2 × 2 × 3 × 5 × 7 × 7
3150 = 2 × 3 × 3 × 5 × 5 × 7
I will write these factors out, all nice and neat, with the factors lined up according to occurrance:
2940: 2×2×3 ×5 ×7×7 3150: 2 ×3×3×5×5×7
This orderly listing, with each factor having its own column, will be doing most of the work for me.
The Greatest Common Factor, the GCF, is the biggest (that is, the "greatest") number that will divide into (that is, the largest number that is a factor of) both 2940 and 3150. In other words, it's the number that contains all the factors *common* to both numbers. In this case, the GCF is the product of all the factors that 2940 and 3150 share.
So, to find the GCF, I just take all the factors that are in both factorizations:
2940: 2×2×3 ×5 ×7×7 3150: 2 ×3×3×5×5×7 ----:---------------- GCF: 2 ×3 ×5 ×7 = 210
Then the GCF is 2 × 3 × 5 × 7 = 210
On the other hand, the Least Common Multiple, the LCM, is the smallest (that is, the "least") number that both 2940 and 3150 will divide into. That is, it is the smallest number that contains both 2940 and 3150 as factors, the smallest number that is a *multiple* that is common to both these values. Therefore, it will be the smallest number that contains every factor in these two numbers.
So, to find the LCM, I just take all the factors from each of the columns in my factor grid:
So, to find the GCF, I just take all the factors that are in both factorizations:
2940: 2×2×3 ×5 ×7×7 3150: 2 ×3×3×5×5×7 ----:---------------- LCM: 2×2×3×3×5×5×7×7 = 44,100
Note that I took each column's factor; I did not use all the copies of a given factor. For instance, while 2940 has two copies of the factor 2 and 3150 has one, I did not take *three* copies of the factor 2. There are only two columns with 2 as their factor, so I took only two copies of that factor when finding the LCM.
Then the LCM is 2 × 2 × 3 × 3 × 5 × 5 × 7 × 7 = 44,100
Affiliate
Many students get confused and accidentally over-duplicate their factors, so let's spend a little extra time on this. Consider two smaller numbers, 4 and 8, and their LCM. The number 4 factors as 2 × 2; 8 factors as 2 × 2 × 2. The LCM needs only have three copies of 2, in order to be divisible by both 4 and 8. That is, the LCM is 8. You do not need to take the three copies of 2 from the 8, and then throw in two extra copies from the 4. This would give you 32. While 32 is a common multiple, because 4 and 8 both divide evenly into 32, 32 is not the LEAST (that is, it is not the smallest) common multiple, because you'd have over-duplicated the 2s when you threw in the extra copies from the 4.
To reiterate: For the GCF, you carry down only those factors that all of the factor listings share (that is, only those factors whose columns are filled in each row); for the LCM, you carry down all the factors, regardless of how many or few of the original values contained that factor in their listings.
Let the nice neat listing keep track of things for you, especially when the numbers get big.
- Find the LCM and GCF of 27, 90, and 84
First, I need to find the prime factorizations:
3)27 2)90 2)84
--- --- ---
3)9 3)45 2)42
-- --- ---
3 3)15 3)21
--- ---
5 7
Then I will list these factorizations neatly, with each copy of each factor getting its own column:
27: 3×3×3 90: 2 ×3×3 ×5 84: 2×2×3 ×7
Then the GCF (being the product of the shared factors — so its the product of all the full columns) and the LCM (being the product of all factors — so its the product of all of the columns) are given by:
GCF: 3 = 3 ---:-------------- 27: 3×3×3 90: 2 ×3×3 ×5 84: 2×2×3 ×7 ---:-------------- LCM: 2×2×3×3×3×5×7 = 3,780
Then my answer is:
GCF: 3
LCM: 3,780
Advertisement
By the way, if you prefer (or if you're lazy, like me), you can omit the "times" signs in your tables, and just list the factors. It'll look like this:
- Find the GCF and LCM of 3, 6, and 8
First I factor the numbers and list their prime factorizations:
3: 3 6: 2 3 8: 2 2 2
Then my GCF and LCM are given by:
GCF: = 1 ---:-------- 3: 3 6: 2 3 8: 2 2 2 ---:-------- LCM: 2 2 2 3 = 24
Note that 3, 6, and 8 share no common factors. While 3 and 6 share a factor, and 6 and 8 share a factor, there is no prime factor that all three of them share. Since 1 divides into everything, then the greatest common factor in this case is just 1. When 1 is the GCF, the numbers are said to be "relatively" prime; that is, they are prime, relative to each other, because they have no common factor (other than the "trivial" factor of 1).
Then my answer is:
GCF: 1
LCM: 24
You can use the Mathway widget below to practice finding the LCM or GCF. Try the entered exercise, or type in your own exercise. Then click the button and select "Find the LCM" from the options, and then compare your answer to Mathway's. (Or jump down to the continuation of this lesson.)
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site, if you'd like to check out their software or get further info.)
The GCF doesn't come up that much at this stage in mathematics, though some books use it for factoring polynomial expressions by having the student find the GCF of all the terms in the polynomial and divide this value out of every term. But the LCM comes up every time you need to find a lowest common denominator for fractions.
The factor technique I demonstrated above works even for polynomial fractions. (The other method for finding the LCM, the "listing" method, will not work for polynomials, which is why you will need to learn the factor method eventually.) If you need to find the LCM of two (or more) polynomials, you can do the exact same procedure as above:
- Find the LCM of x3 + 5x2 + 6x and 2x3 + 4x2
First I factor the polynomials:
x3 + 5x2 + 6x
x(x2 + 5x + 6)
x(x + 2)(x + 3)
...and:
2x3 + 4x2
2x2(x + 2)
Then I list these factors out, nice and neat:
The LCM is the product of the entries from all of the columns:
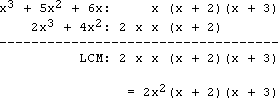
I take two copies of "x", because 2x3 + 4x2 contains two copies. I don't need three copies of "x", because neither polynomial contains three copies. I need only one copy of x + 2, because neither polynomial contains more than just the one copy. I need to account for the 2 from the second polynomial and the x + 3 from the first polynomial.
LCM: 2x2(x + 2)(x + 3).
URL: https://www.purplemath.com/modules/lcm_gcf.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()