Numeric Approximation of a Zero: The Quicker Way
Purplemath
You may have noticed that always using the midpoint of the interval generated some pretty long numbers for my inputs. My computations weren't too hard, because I was making intelligent use of my calculator. But there were times when it was pretty obvious that I could have picked better, and easier, x-values, and still gotten the same answer.
Content Continues Below
Is there an easier way than the midpoint method?
Affiliate
Advertisement
The midpoint method for numerical approximations can take more time and effort to complete than is actually necessary. If you look at the graph (in your calculator), you can pick your own interval endpoints, which is easier and faster than the midpoint method.
If you're working with a calculator that doesn't allow for the symbolic calculations of the polynomial for a given value of x, then choosing x-values with fewer decimal places could be especially handy.
So let's find the polynomial's zero again, but this time we'll go to the trouble of picking our the x-values, instead of just mindlessly always using the midpoint.
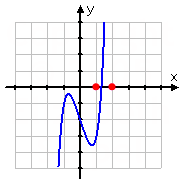
- Find the zero of y = x5 + x3 − 3x − 2, accurate to three decimal places, on the interval 1 ≤ x ≤ 2.
From the graph, I can see that the zero is definitely between x = 1 and x = 2.
Affiliate
I'll find the corresponding y-values:
x = 1: y = −3
x = 2: y = 32
This confirms what the graph told me, but this also tells me that the zero is likely to be a lot closer to x = 1 than to x = 2. Why? Because −3 is a lot closer to zero than is 32.
Since the zero is closer to x = 1, I'll try x = 1.4.
x = 1.4: y = 1.92224
This gets me a lot closer to the axis, but this y-value is positive so the zero is still lower. I'll try x = 1.2:
x = 1.2: y = −1.398369
That's nearly as negative as the last y-value was positive. Okay, so the zero is above x = 1.2 and below x = 1.4. I'll try x = 1.3:
x = 1.3: y = 0.00993
Oooo; that's pretty good. Okay, so I'm really close to the polynomial's zero, but I'm still a little high. I'll edge down by hundredths and try x = 1.29:
x = 1.29: y = −0.151005035...
That took me further from the axis, and below. So the zero is higher, and probably a lot closer to 1.300 than to 1.290. So I'll try x = 1.297:
x = 1.297: y = −0.0388891527...
This y-value is closer to zero, but I'm still too low, and x = 1.300 got me a bit closer still, so I'll try x = 1.299:
x = 1.299: y = −0.006394647...
I'm getting closer, but I'm still too low. I've noticed that 1.3000 was not quite as close to the zero as was 1.2990, but the polynomial also seems to grow faster after the zero than before it, so I'll split the difference and see what I get:
x = 1.2995: y = 0.001761215...
Okay, now I'm too high again, but I'm getting pretty close. Lemme edge down a bit:
x = 1.2994: y = 0.000129009...
x = 1.2993: y = −0.001502678...
Finally! I've managed to bracket the zero between two x-values that have the same first three decimal places. That's all the accuracy I need, so I'm done.
x = 1.299
As you can see, by picking my own x-values, I was able to simplify and shorten my computations. But I did have to pay attention to what I was doing, or I could have ended up picking lots of fairly useless values and taking nearly as long as I would have by using the midpoint process. Either way, though, numerically approximating zeroes isn't terribly complicated; it's just long and and a bit tedious.
Content Continues Below
If they don't tell you "look between here and here for the zero" and you don't have a graphing calculator, you may have to do a little more preliminary work on your own to find the initial interval, but the general process will still be the same.
- Approximate the zero of y = −0.1x5 + 0.3x4 − 0.2x2 + 0.3x − 9.1, accurate to two decimal places.
The first thing I have to do is figure out the general area of the zero. Without a graph and without interval endpoints being given to me, I'll have to use what I know about polynomials to judge the values I get. I'll try a few values in the vicinity of the origin:
x = 0: y = −9.1 (I'm below the axis)
x = 1: y = −8.8 (The graph is coming back up toward the axis)
x = 3: y = −10 (The graph is heading back down; I may be moving the wrong way)
x = 5: y = −137.6 (Okay, yeah; this has got to be the wrong direction; I'll head negative)
x = −1: y = −9.2 (This is about the same as where I started)
x = −2: y = −2.5 (The graph is heading back up toward the axis)
x = −3: y = 36 (The polynomial is finally positive)
Bingo! I've found a sign change, so a zero of the polynomial is somewhere between x = −3 and x = −2. Also, the polynomial is above the axis at the lower x-value, so I know the graph goes down as it crosses the axis. Then a negative y-value will mean that my x-value was too high, and a positive y-value will mean that my x-value was too low. In other words, the signs on the outputs will tell me in which direction I need to move.
Since y = −2.5 (at x = −2) is a lot closer to zero than is y = 36 (at x = −3), I'm going to guess that the zero must be a lot closer to x = −2, so I'll test some values in the tenths:
x = −2.1: y = −0.693469 (I'm getting closer to the axis; I'll move down a bit)
x = −2.2: y = 1.453312 (Now I've gone too far; I've crossed the axis)
Okay, now I know the zero is between x = −2.2 and x = −2.1, and it looks like it's closer to x = −2.1. I'll work my way down into the hundredths:
x = −2.13: y = −0.0870641... (I'm really close, but I'm still below the axis; I'll move down)
x = −2.14: y = 0.1220663... (I'm not quite as close, but I have crossed the axis)
The sign change tells me that the zero is bracketed by x = −2.14 and x = −2.13, with the polynomial being closer to the axis at x = −2.13. I'll test values in the thousandths:
x = −2.133: y = −0.02469719... (I've already crossed the axis, so I need to back up)
x = −2.134: y = −0.003837470... (Still negative, so I need to back up a little more)
x = −2.135: y = 0.0170576798... (The polynomial is back above the axis)
Now I have the zero bracketed between −2.135 and −2.134, numbers that have the same first two decimal places, so I'm done.
x = −2.13
If you're writing a computer program or graphing-calculator program to find numerical approximations, use the midpoint process: it's mindless and rote, which is what you need for an automated process like a program. If your text specifies the method you should use, you should stick with that. Otherwise, use whichever method you prefer. Just allow yourself some time, and be sure to write down your steps carefully. About the only problem you can really have with this process would come from copying down a number wrong. As long as you're neat and don't rush, you should do fine.
URL: https://www.purplemath.com/modules/numeric2.htm
You can use the Mathway widget below to practice numerical approximation. Try the entered exercise, or type in your own exercise. Then click the button and select "Find the Roots (Zeros)" to compare your answer to Mathway's.
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()




