Numerical
Approximation of Zeroes: The Midpoint
Method (page
1 of 2)
You can always find the
exact zeroes of a quadratic equation, because you have a formula: The
Quadratic Formula.
There are formulas for cubic and quartic equations, but they're so complicated
that you'll probably never see them, let alone use them. For polynomial
equations of degrees higher than 4,
there are no general formulas at all.
When you are asked (in
an algebra class) to find the zeroes (the x-intercepts,
solutions, or roots) of a polynomial equation, you will almost always
be given a polynomial that is actually solvable
in some straightforward manner. But most polynomials (in "real life")
aren't solvable. How do you find their zeroes? You don't, exactly; instead,
you find a numerical approximation to some degree of accuracy. (This "to
some degree of accuracy" answer is what you get when you punch buttons
on your graphing calculator to find the root of a graphed equation.) How
does this work?
Advertisement
The secret to approximating
zeroes is to use the "continuity property" of polynomials. This
property (or "trait") of polynomials says that, if your polynomial
equals, say, 5
at some value of x
and equals, say, 10
at some other value of x,
then the polynomial takes on every value between 5
and 10
because polynomials are continuous (connected) lines. They don't have
gaps or jumps or angles or elbows. They don't do anything hinky or unexpected.
They're just nice smooth solid curvy lines.
In particular, if your polynomial
is negative (below the x-axis)
at one spot and positive (above the x-axis)
at another spot, then it has to be zero somewhere in between, because
zero falls between the negatives and the positives.
Look
at the polynomial function y
= x5 + x3 – 3x – 2:
You can quickly see
from the graph that the polynomial is negative (below the axis)
at x
= 1 and positive
(above the axis) at x
= 2. For x
= 1, y
= –3; for x
= 2, y
= 32. Then the
polynomial must be zero (it must cross the axis) somewhere in
between x
= 1 and x
= 2. To find
the zero, you would start looking inside this interval.
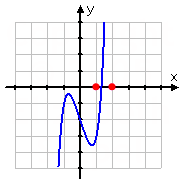
In practice, you'll probably
be given x-values
to use as your starting points, rather than having to find them from a
graph. One of the x-values
will give a negative value for the polynomial and the other will give
a positive value. This is similar to when you use your calculator to find
zeroes on a graph, and the calculator asks you to pick left- and right-hand
bounds for the zero.
There are two methods for
narrowing in on a polynomial's zero: using midpoints, and picking clever
values for x.
I'll show midpoints first.
Find the root of the
polynomial x5
+ x3 – 3x
– 2, accurate
to three decimal places.
Right now, I only know
that the zero is somewhere between x
= 1 and x
= 2. To get closer
to the zero by using midpoints, I will split the difference, literally:
I'll try x
= 1.5.
At
x
= 1.5, I get y
= 4.46875.
The actual y-value
isn't as important as the sign: since the polynomial is positive
here, the graph is above the axis. Since the polynomial is positive
at x
= 1.5 and x
= 2, but is
negative at x
= 1, I now
know that the zero has to be between x
= 1 and
x
= 1.5.
(The new interval
endpoints, bracketing the zero, are marked in red on the graph.)
So I'll split the
difference again. The halfway point between x
= 1 and x
= 1.5 is x
= 1.25. At
this point, y
= –0.745117,
approximately. The important thing to note is that this is a
negative y-value.
The polynomial is positive at the x
= 1.5 endpoint,
so the new bounds on my interval are x
= 1.25 and
x
= 1.5.
This
interval is halved by x
= 1.375. (I
am taking the average of the two x-values
to find my midpoints.) This gives me y
= 1.38950,
approximately, which is positive. So I'll keep x
= 1.25 as
the lower endpoint and use x
= 1.375 as
the new upper boundary.
The midpoint
between x
= 1.25 and x
= 1.375 is x
= 1.3125, which gives y
= 0.218389, approximately.
Since the polynomial is positive here, I'll keep x
= 1.25 as the lower boundary
and use x
= 1.3125 as the new upper
boundary.
The midpoint
between x
= 1.25 and x
= 1.3125 is x
= 1.28125, which gives y
= –0.287664,
approximately. Since the polynomial is negative here, I'll keep
x
= 1.3125 as the upper
boundary and use x
= 1.28125 as the new lower
boundary.
The midpoint between x
= 1.28125 and x
= 1.3125 is x
= 1.296875, which gives y
= –0.40913,
approximately. Since the polynomial is negative here, I'll keep
x
= 1.3125 as the upper
boundary and use x
= 1.296875 as the new lower
boundary.
As you can see, I'm getting a
lot closer to where the zero is.
The midpoint
between x
= 1.296875 and x
= 1.3125 is x
= 1.3046875, which gives
y = 0.87143,
approximately. Since the polynomial is positive here, I'll keep
x
= 1.296875 as the lower
boundary and use x
= 1.3046875 as the new upper
boundary.
The midpoint
between x
= 1.296875 and x
= 1.3046875 is x
= 1.30078125, which gives
y = 0.0227196,
approximately. Since the polynomial is positive here, I'll keep
x
= 1.296875 as the lower boundary
and use x
= 1.30078125 as the new upper
boundary.
You've probably got the idea by now,
so I'll just show the rest of my computations:
The last midpoint becomes
the new lower boundary of the interval, and I now have bracketed the
polynomial's zero between x
= 1.299316407 and
x
= 1.299804688. Since
these two x-values
agree in the first three decimal places, I'm done.
The polynomial's
zero, to three decimal places of accuracy, is at x
= 1.299.
Stapel, Elizabeth.
"Numerical Approximation of Zeroes: The Midpoint Method." Purplemath. Available from https://www.purplemath.com/modules/numeric.htm.
Accessed
